Όπως είχα ήδη υπαινιχθεί, η δεύτερη ακραία περίπτωση (τετραπλεύρου με μήκη δύο διαδοχικών πλευρών

και ισοκάθετες διαγωνίους) είναι λιγότερο προφανής από την πρώτη, και στην αμέσως προηγούμενη δημοσίευση μου η εύρεση της έχει γίνει πειραματικά (WolframAlpha). Αν θέλουμε μία ακριβή λύση εργαζόμαστε, με αναφορά στο συνημμένο, ως εξής:
Αντικαθιστώντας τις

και

στην

λαμβάνουμε, ύστερα από ύψωση στο τετράγωνο και λίγες πράξεις, την διτετράγωνη

και από αυτήν την

[Η άλλη θετική λύση της διτετράγωνης απορρίπτεται επειδή καθιστά αρνητικό το δεξιό σκέλος της

(που προκύπτει στην πορεία μας προς την διτετράγωνη και αμέσως πριν την ύψωση στο τετράγωνο).]
Όσα έχω γράψει σ αυτήν την συζήτηση γενικεύονται άμεσα στο εξής αποτέλεσμα:
Αν

είναι το κοινό μήκος ισοκαθέτων διαγωνίων μη εκφυλισμένου κυρτού τετραπλεύρου με γνωστά μήκη διαδοχικών πλευρών

τότε

με τα δύο φράγματα να είναι τα καλύτερα δυνατά (όπως δείχνουν τα παραδείγματα μας).
Η παραπάνω ανισότητα μας δίνει και το ελάχιστο και μέγιστο δυνατό εμβαδόν για κυρτό τετράπλευρο με ισοκάθετες διαγωνίους και γνωστά μήκη δύο διαδοχικών πλευρών. Προκύπτει επίσης ότι σε κάθε κυρτό τετράπλευρο με ισοκάθετες διαγωνίους οποιεσδήποτε δύο διαδοχικές πλευρές μηκών

οφείλουν να ικανοποιούν την

(να έχουν δηλαδή λόγο

ανάμεσα στις

και

, όπου

η χρυσή τομή).
Γιώργος Μπαλόγλου
 κατασκευάστηκε με κάθετες διαγωνίους και πλευρές
κατασκευάστηκε με κάθετες διαγωνίους και πλευρές  .
.

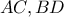 αν και μόνον αν
αν και μόνον αν  , οπότε άμεσα προκύπτει η
, οπότε άμεσα προκύπτει η  .
. η τομή των καθέτων διαγωνίων
η τομή των καθέτων διαγωνίων  , τότε από το Πυθαγόρειο Θεώρημα έχουμε
, τότε από το Πυθαγόρειο Θεώρημα έχουμε

 ,
, καθίσταται ισοδύναμη προς την
καθίσταται ισοδύναμη προς την  .
. προκύπτει η
προκύπτει η  .
. τεταρτοβάθμιος είναι στην πραγματικότητα δευτεροβάθμιος, ανάγεται δηλαδή η
τεταρτοβάθμιος είναι στην πραγματικότητα δευτεροβάθμιος, ανάγεται δηλαδή η 




 , και όχι και τόσο φανερό ότι μηδενίζεται ΚΑΙ ο συντελεστής του
, και όχι και τόσο φανερό ότι μηδενίζεται ΚΑΙ ο συντελεστής του 
 ΔΕΝ είναι αποδεκτή ... επειδή στο δεύτερο στάδιο* της αναγωγής της αρχικής εξίσωσης στην διτετράγωνη,
ΔΕΝ είναι αποδεκτή ... επειδή στο δεύτερο στάδιο* της αναγωγής της αρχικής εξίσωσης στην διτετράγωνη,
 ... καθιστά ΚΑΙ τα δύο σκέλη αρνητικά, άρα δεν έχουμε πρόβλημα!]
... καθιστά ΚΑΙ τα δύο σκέλη αρνητικά, άρα δεν έχουμε πρόβλημα!] και
και  ): ποια είναι η ανώτατη δυνατή τιμή -- ακριβέστερα, το ελάχιστο άνω φράγμα -- που μπορεί να λάβει η τρίτη δοθείσα πλευρά; [Πειραματική επίλυση στο WolframAlpha και γεωμετρική ματιά που απλοποιεί τα πράγματα -- τι γίνεται με την κατώτατη δυνατή τιμή της τρίτης πλευράς;]
): ποια είναι η ανώτατη δυνατή τιμή -- ακριβέστερα, το ελάχιστο άνω φράγμα -- που μπορεί να λάβει η τρίτη δοθείσα πλευρά; [Πειραματική επίλυση στο WolframAlpha και γεωμετρική ματιά που απλοποιεί τα πράγματα -- τι γίνεται με την κατώτατη δυνατή τιμή της τρίτης πλευράς;] και ισοκάθετες διαγωνίους) είναι λιγότερο προφανής από την πρώτη, και στην αμέσως προηγούμενη δημοσίευση μου η εύρεση της έχει γίνει πειραματικά (WolframAlpha). Αν θέλουμε μία ακριβή λύση εργαζόμαστε, με αναφορά στο συνημμένο, ως εξής:
και ισοκάθετες διαγωνίους) είναι λιγότερο προφανής από την πρώτη, και στην αμέσως προηγούμενη δημοσίευση μου η εύρεση της έχει γίνει πειραματικά (WolframAlpha). Αν θέλουμε μία ακριβή λύση εργαζόμαστε, με αναφορά στο συνημμένο, ως εξής: και
και  στην
στην  λαμβάνουμε, ύστερα από ύψωση στο τετράγωνο και λίγες πράξεις, την διτετράγωνη
λαμβάνουμε, ύστερα από ύψωση στο τετράγωνο και λίγες πράξεις, την διτετράγωνη

 (που προκύπτει στην πορεία μας προς την διτετράγωνη και αμέσως πριν την ύψωση στο τετράγωνο).]
(που προκύπτει στην πορεία μας προς την διτετράγωνη και αμέσως πριν την ύψωση στο τετράγωνο).] είναι το κοινό μήκος ισοκαθέτων διαγωνίων μη εκφυλισμένου κυρτού τετραπλεύρου με γνωστά μήκη διαδοχικών πλευρών
είναι το κοινό μήκος ισοκαθέτων διαγωνίων μη εκφυλισμένου κυρτού τετραπλεύρου με γνωστά μήκη διαδοχικών πλευρών  τότε
τότε
 οφείλουν να ικανοποιούν την
οφείλουν να ικανοποιούν την  (να έχουν δηλαδή λόγο
(να έχουν δηλαδή λόγο  ανάμεσα στις
ανάμεσα στις  και
και  , όπου
, όπου  η χρυσή τομή).
η χρυσή τομή).