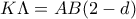 αφού
αφού 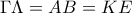 και
και 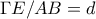 . Όμοια μπορούμε να υπολογίσουμε όλες τις πλευρές του εσωτερικού πενταγώνου. Παρατηρούμε ότι το εσωτερικό πεντάγωνο είναι όμοιο με το αρχικό με λόγο αναλογία
. Όμοια μπορούμε να υπολογίσουμε όλες τις πλευρές του εσωτερικού πενταγώνου. Παρατηρούμε ότι το εσωτερικό πεντάγωνο είναι όμοιο με το αρχικό με λόγο αναλογία 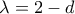 , επομένως o λόγος το εμβαδών θα είναι:
, επομένως o λόγος το εμβαδών θα είναι: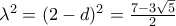
Συντονιστής: gbaloglou
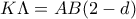 αφού
αφού 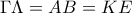 και
και 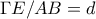 . Όμοια μπορούμε να υπολογίσουμε όλες τις πλευρές του εσωτερικού πενταγώνου. Παρατηρούμε ότι το εσωτερικό πεντάγωνο είναι όμοιο με το αρχικό με λόγο αναλογία
. Όμοια μπορούμε να υπολογίσουμε όλες τις πλευρές του εσωτερικού πενταγώνου. Παρατηρούμε ότι το εσωτερικό πεντάγωνο είναι όμοιο με το αρχικό με λόγο αναλογία 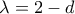 , επομένως o λόγος το εμβαδών θα είναι:
, επομένως o λόγος το εμβαδών θα είναι: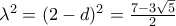
Με αφορμή αυτό, ο Γιώργος Τσίντσιφας, που συνάντησα για άλλους λόγους σήμερα το πρωί, προτείνει την εξής προσέγγιση: με δεδομένο ότι κάθε κυρτό πεντάγωνο εγγράφεται σε έλλειψη, και κάθε έλλειψη απεικονίζεται ομοπαραλληλικά (affinely) σε κύκλο, να διερευνηθεί η πιθανότητα αναγωγής του προβλήματος σε πεντάγωνα εγγεγραμμένα σε κύκλο. [Πιθανολογώ ότι η προσέγγιση Τσίντσιφα επιλύει το πρόβλημα επαληθεύοντας την παραπάνω εικασία, αλλά προς το παρόν δεν έχω χρόνο να το δω.]gbaloglou έγραψε:Πολύ ωραία, με την συνδρομή του Παύλου και του Mathematica έχουμε φτάσει σε μια πολύ όμορφη εικασία: ο λόγος των εμβαδών μεγιστοποιείται σε εκείνα ακριβώς τα πεντάγωνα όπου η κάθε διαγώνιος είναι παράλληλη προς μία πλευρά!
Μέλη σε αυτήν τη Δ. Συζήτηση: SemrushBot και 1 επισκέπτης