 δίνεται ένα σταθερό σημείο
δίνεται ένα σταθερό σημείο  . Τα σημεία
. Τα σημεία  κινούνται πάνω στον κύκλο, έτσι ώστε
κινούνται πάνω στον κύκλο, έτσι ώστε  . Αν οι εφαπτόμενες του κύκλου στα
. Αν οι εφαπτόμενες του κύκλου στα  τέμνονται στο
τέμνονται στο  , να βρεθεί ο γεωμετρικός τόπος του
, να βρεθεί ο γεωμετρικός τόπος του  .
.Συντονιστής: gbaloglou
 δίνεται ένα σταθερό σημείο
δίνεται ένα σταθερό σημείο  . Τα σημεία
. Τα σημεία  κινούνται πάνω στον κύκλο, έτσι ώστε
κινούνται πάνω στον κύκλο, έτσι ώστε  . Αν οι εφαπτόμενες του κύκλου στα
. Αν οι εφαπτόμενες του κύκλου στα  τέμνονται στο
τέμνονται στο  , να βρεθεί ο γεωμετρικός τόπος του
, να βρεθεί ο γεωμετρικός τόπος του  .
. είναι
είναι  και η απόσταση του σημείου
και η απόσταση του σημείου  από το κέντρο του είναι
από το κέντρο του είναι 
 είναι κύκλος με κέντρο
είναι κύκλος με κέντρο  επί της προέκτασης της
επί της προέκτασης της  προς το
προς το  και σε απόσταση
και σε απόσταση  και ακτίνα
και ακτίνα 
george visvikis έγραψε: Στο εσωτερικό ενός κύκλουδίνεται ένα σταθερό σημείο
. Τα σημεία
κινούνται πάνω στον κύκλο, έτσι ώστε
. Αν οι εφαπτόμενες του κύκλου στα
τέμνονται στο
, να βρεθεί ο γεωμετρικός τόπος του
.
 ,
,  η ακτίνα του κύκλου και
η ακτίνα του κύκλου και  τα μέσα των
τα μέσα των  .
. διαγράφει
διαγράφει  .
. του κύκλου
του κύκλου  και δύναμη αντιστροφής
και δύναμη αντιστροφής  δίδει τον ζητούμενο γεωμετρικό τόπο .
δίδει τον ζητούμενο γεωμετρικό τόπο . .
. και έστω ότι τέμνουν τον κύκλο
και έστω ότι τέμνουν τον κύκλο  στα σημεία
στα σημεία  . Από τα σημεία
. Από τα σημεία  φαίρνουμε τις εφαπτομένες προς αυτόν τον κύκλο οι οποίες σχηματίζουν το τετράπλευρο
φαίρνουμε τις εφαπτομένες προς αυτόν τον κύκλο οι οποίες σχηματίζουν το τετράπλευρο  . Για το τετράπλευρο αυτό και για τις γωνίες του όπως φαίνονται στο σχήμα έχουμε:
. Για το τετράπλευρο αυτό και για τις γωνίες του όπως φαίνονται στο σχήμα έχουμε: (1)
(1) (2)
(2) (3)
(3)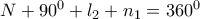 (4)
(4)
 από το θεώρημα χορδής και εφαπτομένης ισουται με μία από τις εγγεγραμμένες γωνίες του εγγεγραμένου τετραπλεύρου
από το θεώρημα χορδής και εφαπτομένης ισουται με μία από τις εγγεγραμμένες γωνίες του εγγεγραμένου τετραπλεύρου  . Έτσι το αθροισμά τους είναι ίσο με
. Έτσι το αθροισμά τους είναι ίσο με  . Eπομένως
. Eπομένως  και το
και το  είναι εγγράψιμο.
είναι εγγράψιμο. του περιγγεγραμμένου κύκλου του
του περιγγεγραμμένου κύκλου του  μπορεί να θεωρηθεί κορυφή του. Οπότε ο ζητούμενος γεωμετρικός τόπος είναι αυτός ο κύκλος.
μπορεί να θεωρηθεί κορυφή του. Οπότε ο ζητούμενος γεωμετρικός τόπος είναι αυτός ο κύκλος. τον αρχικό κύκλο,
τον αρχικό κύκλο,  τον κύκλο του γεωμετρικού τόπου και θέτω
τον κύκλο του γεωμετρικού τόπου και θέτω  . Όπως φαίνεται και από την προσέγγιση του Αλέξανδρου (που δεν είναι καθόλου ημιτελής, απλώς δεν δίνει κέντρο και ακτίνα του κύκλου), το τετράπλευρο
. Όπως φαίνεται και από την προσέγγιση του Αλέξανδρου (που δεν είναι καθόλου ημιτελής, απλώς δεν δίνει κέντρο και ακτίνα του κύκλου), το τετράπλευρο  είναι αμφιγράψιμο.
είναι αμφιγράψιμο. που ανήκει στην ευθεία
που ανήκει στην ευθεία  (τα σημεία
(τα σημεία  εκατέρωθεν του
εκατέρωθεν του  ), σε απόσταση
), σε απόσταση  και έχει ακτίνα
και έχει ακτίνα 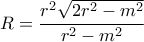 . Στη συνέχεια, με απαλοιφή του
. Στη συνέχεια, με απαλοιφή του  , κατέληξε στον γνωστό τύπο:
, κατέληξε στον γνωστό τύπο: 
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 8 επισκέπτες