Στο παραπάνω σχήμα το τετράπλευρο
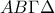 είναι τετράγωνο και το
είναι τετράγωνο και τοτρίγωνο
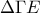 ισοσκελές με
ισοσκελές με  . Αν
. Αν  ,
,δείξτε ότι
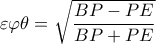 .
.Συντονιστής: gbaloglou
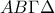 είναι τετράγωνο και το
είναι τετράγωνο και το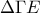 ισοσκελές με
ισοσκελές με  . Αν
. Αν  ,
,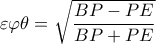 .
. είναι ισοσκελές, είναι
είναι ισοσκελές, είναι  , οπότε είναι
, οπότε είναι  .
.



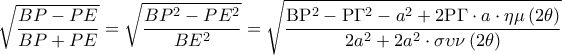

 .
.

 . Γράφω το ημικύκλιο
. Γράφω το ημικύκλιο 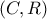 που διέρχεται
που διέρχεται  και έστω
και έστω  το αντιδιαμετρικό του
το αντιδιαμετρικό του  . Η εφαπτομένη του ημικυκλίου
. Η εφαπτομένη του ημικυκλίου  τέμνει την ευθεία
τέμνει την ευθεία  στο
στο  . Αν
. Αν  το μέσο του
το μέσο του 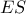 προφανώς
προφανώς  . Επειδή
. Επειδή 
 ) θα είναι
) θα είναι  οπότε
οπότε  .
. και άρα
και άρα  .
.ΑνΦανης Θεοφανιδης έγραψε:432.png
Καλησπέρα.
Στο παραπάνω σχήμα το τετράπλευροείναι τετράγωνο και το
τρίγωνοισοσκελές με
. Αν
,
δείξτε ότι.
 οπότε
οπότε 


 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες