 έχει
έχει  και
και  . Για το σημείο
. Για το σημείο  της
της  ισχύει
ισχύει  .
.Το
 ενώ το
ενώ το  είναι εφαπτόμενο στο
είναι εφαπτόμενο στο  του τόξου που ορίζουν τα
του τόξου που ορίζουν τα  .
.Στην προέκταση της
 παίρνουμε
παίρνουμε  . Να δειχθεί ότι
. Να δειχθεί ότι  .
.Ευχαριστώ , Γιώργος .
Συντονιστής: gbaloglou
 έχει
έχει  και
και  . Για το σημείο
. Για το σημείο  της
της  ισχύει
ισχύει  .
. ενώ το
ενώ το  είναι εφαπτόμενο στο
είναι εφαπτόμενο στο  του τόξου που ορίζουν τα
του τόξου που ορίζουν τα  .
. παίρνουμε
παίρνουμε  . Να δειχθεί ότι
. Να δειχθεί ότι  .
.Γιώργο καλησπέρα! Μου άρεσε ιδιαίτερα αυτό το πρόβλημα. Δυστυχώς δεν κατάφερα να αποφύγων τη "σκληρή" τριγωνομετρία η οποία (μάλλον δύσκολα θα αποφευχθεί) υποθέτω ότι είναι επιτρεπτή αν κρίνω από το φάκελο στον οποίο έχει τεθεί το όμορφο αυτό πρόβλημα!Γιώργος Μήτσιος έγραψε:Καλημέρα .
Το τρίγωνοέχει
και
. Για το σημείο
της
ισχύει
.Το
ενώ το
είναι εφαπτόμενο στο
του τόξου που ορίζουν τα
.Στην προέκταση της
παίρνουμε
. Να δειχθεί ότι
.
Ευχαριστώ , Γιώργος .
 το σημείο τομής (εκτός του
το σημείο τομής (εκτός του  ) της
) της  με τον περίκυκλο του τριγώνου
με τον περίκυκλο του τριγώνου  και
και  οι ορθές προβολές του
οι ορθές προβολές του  στις
στις  αντίστοιχα. Από τη συμμετρία (λόγω του ισοσκελούς τριγώνου) και τα δεδομένα του προβλήματος προκύπτει εύκολα ότι
αντίστοιχα. Από τη συμμετρία (λόγω του ισοσκελούς τριγώνου) και τα δεδομένα του προβλήματος προκύπτει εύκολα ότι .
. 














 . Από την
. Από την  σύμφωνα με το [/color][color=#000000][b][i]Stathis Ko ... b][/color] προκύπτει ότι
σύμφωνα με το [/color][color=#000000][b][i]Stathis Ko ... b][/color] προκύπτει ότι  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. μέσο της
μέσο της  ,άρα
,άρα  .
. το κέντρο του κύκλου που διέρχεται από τα σημεία
το κέντρο του κύκλου που διέρχεται από τα σημεία  . Τότε
. Τότε  ,
, ,
,  , οπότε
, οπότε  .
.  το συμμετρικό του
το συμμετρικό του  ως προς τη
ως προς τη  και σχηματίζω το ισοσκελές τρίγωνο
και σχηματίζω το ισοσκελές τρίγωνο  με
με . Τότε τα τρίγωνα
. Τότε τα τρίγωνα  είναι ίσα διότι
είναι ίσα διότι  . Άρα
. Άρα  .
. είναι ίσα , άρα
είναι ίσα , άρα  και
και  .
. είναι ίσα διότι
είναι ίσα διότι  .
. .
. και
και  .Στο ορθ. τρίγωνο
.Στο ορθ. τρίγωνο  είναι
είναι  .
. , στο
, στο 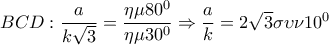
 .
. ενώ και
ενώ και  συνεπώς ,όπως και ΕΔΩ
συνεπώς ,όπως και ΕΔΩ παίρνουμε
παίρνουμε  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 13 επισκέπτες