 είναι η διχοτόμος και
είναι η διχοτόμος και  το ύψος τριγώνου
το ύψος τριγώνου  Αν
Αν 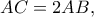 να βρείτε το είδος του
να βρείτε το είδος του τριγώνου για το οποίο ελαχιστοποιείται η γωνία
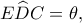 καθώς και την ελάχιστη τιμή της
καθώς και την ελάχιστη τιμή της 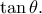
Συντονιστής: gbaloglou
 είναι η διχοτόμος και
είναι η διχοτόμος και  το ύψος τριγώνου
το ύψος τριγώνου  Αν
Αν 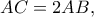 να βρείτε το είδος του
να βρείτε το είδος του 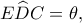 καθώς και την ελάχιστη τιμή της
καθώς και την ελάχιστη τιμή της 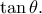
Για το α)george visvikis έγραψε: ↑Τρί Ιαν 16, 2024 1:24 pmΕλαχιστοποίηση αμβλείας.png
είναι η διχοτόμος και
το ύψος τριγώνου
Αν
να βρείτε το είδος του
τριγώνου για το οποίο ελαχιστοποιείται η γωνίακαθώς και την ελάχιστη τιμή της
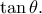
 . Και προς το αυτό μέρος , το ημικύκλιο διαμέτρου
. Και προς το αυτό μέρος , το ημικύκλιο διαμέτρου  και το ημικύκλιο διαμέτρου
και το ημικύκλιο διαμέτρου  με
με  το αρμονικό συζυγές του
το αρμονικό συζυγές του  ως προς τα
ως προς τα  ..
.. 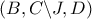 να είναι αρμονική .
Το μεν
να είναι αρμονική .
Το μεν  ανήκει σ αυτό το ημικύκλιο. Επί της ουσίας έχω Απολλώνιο ημικύκλιο, το δε
ανήκει σ αυτό το ημικύκλιο. Επί της ουσίας έχω Απολλώνιο ημικύκλιο, το δε  στο διαμέτρου
στο διαμέτρου  ..
..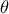 , η
, η 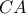 γίνεται εφαπτομένη του Απολλώνιου ημικυκλίου .
γίνεται εφαπτομένη του Απολλώνιου ημικυκλίου .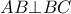 . Δηλαδή το τρίγωνο
. Δηλαδή το τρίγωνο  είναι ορθογώνιο στο
είναι ορθογώνιο στο  .
.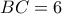 και προκύπτουν αβίαστα τα νούμερα που φαίνονται στο σχήμα .
και προκύπτουν αβίαστα τα νούμερα που φαίνονται στο σχήμα .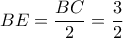 ,
, 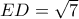 ( Θ. συνημίτονου στο
( Θ. συνημίτονου στο 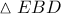 ).
). 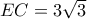 (Π. Θ. στο
(Π. Θ. στο 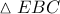 ). Μετά από Θ. συνημίτονου στο
). Μετά από Θ. συνημίτονου στο  έχω :
έχω :
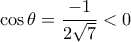 και άρα η γωνία
και άρα η γωνία 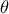 είναι αμβλεία . Έτσι από τον γνωστό τύπο ,
είναι αμβλεία . Έτσι από τον γνωστό τύπο , 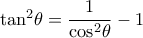 , προκύπτει:
, προκύπτει: 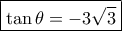 .
. είναι
είναι 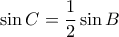
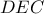 είναι
είναι 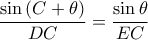
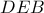 είναι
είναι 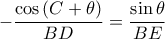
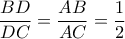 και ότι
και ότι 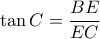 έχουμε
έχουμε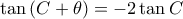
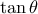 ....
.... 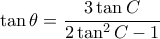
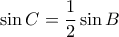 και έτσι η μέγιστη τιμή του
και έτσι η μέγιστη τιμή του 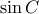 είναι
είναι  , όταν
, όταν 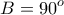 ,
, 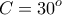 .
. 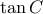 θα είναι
θα είναι 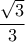
![\displaystyle{f(x)=\frac{3x}{2x^2-1}, x\in \left(0,\frac{\sqrt{3}}{3}\right]} \displaystyle{f(x)=\frac{3x}{2x^2-1}, x\in \left(0,\frac{\sqrt{3}}{3}\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/afb9502423753af72ac39249feb56534.png) είναι γνησίως φθίνουσα,
είναι γνησίως φθίνουσα, 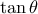 , θα συμβεί όταν η
, θα συμβεί όταν η 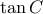 έχει την μέγιστη τιμή της
έχει την μέγιστη τιμή της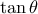 επιτυγχάνεται στο ορθογώνιο τρίγωνο και είναι ίση με
επιτυγχάνεται στο ορθογώνιο τρίγωνο και είναι ίση με 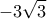


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες