Μια προσέγγιση για το (α). Με ταλαιπώρησε πολύ και ακόμα δεν είναι πλήρως ολοκληρωμένη.
Ξεκινάμε με την περίπτωση

. Αυτό είναι και το σημείο στο οποίο δεν μπόρεσα να βρω λύση. Βάζω μόνο κάποιες σκέψεις.
Η εξίσωση γίνεται:

. Εύκολα με

και

μπορούμε να δούμε ότι
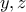
περιττοί. Από εκεί και πέρα δεν ξέρω τι να κάνω και το αφήνω ανοικτό για όποιον θέλει να
προσπαθήσει.
Για

η εξίσωση γίνεται:
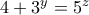
. Με

παίρνω

και με

παίρνω

. Έτσι η εξίσωση γίνεται:

.
Προκύπτουν κάποια συστήματα τα οποία όμως δεν δίνουν λύση(δεν τα γράφω για εξοικονόμηση χρόνου).
Έστω τώρα

.
Με

έχουμε ότι

. Επομένως

. Ακόμα, αφού

είναι

. Επομένως θα πρέπει

.
Αν

περιττός έστω

έχουμε

, άτοπο.
Αν

άρτιο, έστω

τότε

, δεκτό.
Άρα

.
Η εξίσωση γίνεται:

.
Επομένως:

με

και

.
Με πρόσθεση κατά μέλη έχουμε:

Αν

θα είχαμε

, άτοπο.
Άρα

.
Επομένως, η εξίσωση γίνεται:

.
Αν

έχουμε

.
Με

έχουμε

, άτοπο.
Άρα
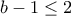
. Εύκολα τώρα παίρνουμε
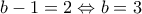
.
Έτσι
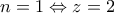
. Τελικά, προκύπτει η λύση

.
Y.Γ.: Θα ήθελα να παρακαλέσω όποιον μπορεί να δει την περίπτωση

γιατί με έχει ταλαιπωρήσει πάρα πολύ...
Πάντα κατ' αριθμόν γίγνονται... ~ Πυθαγόρας
Ψυρούκης Ραφαήλ
 για x,y,z θετικούς ακέραιους(Βασικά έχω δεί πολλά θεωρήματα σχετικά με τις λύσεις της διοφαντικής
για x,y,z θετικούς ακέραιους(Βασικά έχω δεί πολλά θεωρήματα σχετικά με τις λύσεις της διοφαντικής  με a,b,c δοσμένους θετικούς ακέραιους αλλά είναι δυσνόητα)
με a,b,c δοσμένους θετικούς ακέραιους αλλά είναι δυσνόητα) είναι κύβος ακέραιου αριθμού όπου p πρώτος αριθμός
είναι κύβος ακέραιου αριθμού όπου p πρώτος αριθμός


 ,
, 

 τότε δεν έχουμε λύση γιατί το δεξί μέλος προφανώς μεγαλύτερος αριθμός από το αριστερό.
τότε δεν έχουμε λύση γιατί το δεξί μέλος προφανώς μεγαλύτερος αριθμός από το αριστερό. και
και 
 ,
, 
 (η τον
(η τον  ) θα έχουμε τελικά το τριώνυμο ..
) θα έχουμε τελικά το τριώνυμο .. σε
σε  , ευχαριστώ για την επισήμανση παρακάτω.
, ευχαριστώ για την επισήμανση παρακάτω.
 για κάθε
για κάθε 
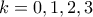 και έχει λύση μόνο για
και έχει λύση μόνο για  οπότε
οπότε  ,
, 

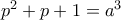 ενώ είναι
ενώ είναι 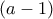 για να καταλήξεις στο τριώνυμο που έχω γράψει στην λύση μου.
για να καταλήξεις στο τριώνυμο που έχω γράψει στην λύση μου. . Αυτό είναι και το σημείο στο οποίο δεν μπόρεσα να βρω λύση. Βάζω μόνο κάποιες σκέψεις.
. Αυτό είναι και το σημείο στο οποίο δεν μπόρεσα να βρω λύση. Βάζω μόνο κάποιες σκέψεις. . Εύκολα με
. Εύκολα με  και
και  μπορούμε να δούμε ότι
μπορούμε να δούμε ότι 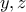 περιττοί. Από εκεί και πέρα δεν ξέρω τι να κάνω και το αφήνω ανοικτό για όποιον θέλει να
περιττοί. Από εκεί και πέρα δεν ξέρω τι να κάνω και το αφήνω ανοικτό για όποιον θέλει να  η εξίσωση γίνεται:
η εξίσωση γίνεται: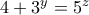 . Με
. Με  και με
και με  παίρνω
παίρνω  . Έτσι η εξίσωση γίνεται:
. Έτσι η εξίσωση γίνεται: .
. .
.  . Ακόμα, αφού
. Ακόμα, αφού  . Επομένως θα πρέπει
. Επομένως θα πρέπει  .
. περιττός έστω
περιττός έστω  έχουμε
έχουμε  , άτοπο.
, άτοπο. τότε
τότε  , δεκτό.
, δεκτό. .
.
 και
και  .
.
 θα είχαμε
θα είχαμε  , άτοπο.
, άτοπο. .
. .
. έχουμε
έχουμε  .
. , άτοπο.
, άτοπο.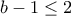 . Εύκολα τώρα παίρνουμε
. Εύκολα τώρα παίρνουμε 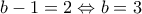 .
.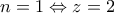 . Τελικά, προκύπτει η λύση
. Τελικά, προκύπτει η λύση  .
. Ραφαήλ.
Ραφαήλ. έχουμε τη λύση
έχουμε τη λύση 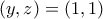 .
. , έχουμε
, έχουμε  αφαιρώντας
αφαιρώντας  .
. είναι περιττό.
είναι περιττό.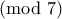 , έχουμε:
, έχουμε: ,
,

 ,
,  ,
,  προκύπτει ότι
προκύπτει ότι  άρτιοι αντίστοιχα.
άρτιοι αντίστοιχα. ,
,  ,
,
 ,
, 
 ,
, 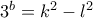 ,
,  όπου
όπου  ,
,  οπότε εύκολα
οπότε εύκολα 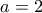 ,
, 
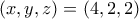
 ομοίως όπως ο jim.jt. για την λύση
ομοίως όπως ο jim.jt. για την λύση 


 οπότε έχουμε να λύσουμε την
οπότε έχουμε να λύσουμε την 
 .
. , άρα
, άρα  , και όμοια
, και όμοια  .
. , έχουμε
, έχουμε  , άρα έχουμε ισότητα, δηλαδή
, άρα έχουμε ισότητα, δηλαδή  , και αφού είναι πρώτοι, ένας είναι
, και αφού είναι πρώτοι, ένας είναι  .
. όχι πρώτος.
όχι πρώτος. και με δοκιμές έχουμε
και με δοκιμές έχουμε 