ΑΣΚΗΣΗ 4
Για τους αριθμούς

ισχύει η σχέση
 α.
α. Να βρεθούν οι αριθμοί

Για τους αριθμούς

που βρήκατε στο α) ερώτημα
β. Να μετατρέψετε το κλάσμα
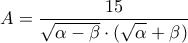
σε ισοδύναμο με ρητό παρονομαστή.
γ. Να υπολογίσετε την τιμή της παράστασης
 δ.
δ. Να υπολογίσετε την τιμή της παράστασης
![\displaystyle{\Delta = \sqrt {\alpha \sqrt[3]{\alpha }} \cdot \sqrt[3]{\alpha } - \beta } \displaystyle{\Delta = \sqrt {\alpha \sqrt[3]{\alpha }} \cdot \sqrt[3]{\alpha } - \beta }](/forum/ext/geomar/texintegr/latexrender/pictures/180210baddf3c406f9015bb8c431a1fb.png) ΑΣΚΗΣΗ 5
ΑΣΚΗΣΗ 5
Δίνεται η εξίσωση

 α.
α. Να βρείτε για ποίες τιμές του

η εξίσωση

έχει δύο πραγματικές και άνισες λύσεις
β.Έστω

και

το άθροισμα και το γινόμενο αντίστοιχα των ριζών της εξίσωσης

. Άν ισχύει

, να προσδιορίσετε την τιμή του

Για την τιμή του

που βρήκατε στο β) ερώτημα,τότε:
γ. Να υπολογίσετε την παράσταση
 δ.
δ. Να κατασκευάσετε εξίσωση δευτέρου βαθμού, με ρίζες τους αριθμούς

και



 η εξίσωση έχει δύο πραγματικές και άνισες λύσεις.
η εξίσωση έχει δύο πραγματικές και άνισες λύσεις. ώστε ο αριθμός
ώστε ο αριθμός ![\displaystyle{x = \sqrt[6]{{2^2 }} \cdot \sqrt {\sqrt[3]{2}} } \displaystyle{x = \sqrt[6]{{2^2 }} \cdot \sqrt {\sqrt[3]{2}} }](/forum/ext/geomar/texintegr/latexrender/pictures/c5bce2d0341b1699c2db3cdb236af644.png) να είναι ρίζα της
να είναι ρίζα της 
 έχει δύο πραγματικές ρίζες
έχει δύο πραγματικές ρίζες  , να βρεθεί το
, να βρεθεί το  , ώστε
, ώστε 


 αρα
αρα  πρεπει ομως
πρεπει ομως 
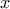 ισουται με
ισουται με ![\displaystyle{ x= \sqrt[6]{2^2} \cdot \sqrt[6]{2} \Leftrightarrow x= \sqrt[6]{2^2 \cdot 2} \Leftrightarrow x=\sqrt[6]{2^3} \Leftrightarrow x=\sqrt[2]{2} } \displaystyle{ x= \sqrt[6]{2^2} \cdot \sqrt[6]{2} \Leftrightarrow x= \sqrt[6]{2^2 \cdot 2} \Leftrightarrow x=\sqrt[6]{2^3} \Leftrightarrow x=\sqrt[2]{2} }](/forum/ext/geomar/texintegr/latexrender/pictures/4478dae033df69dce5ff3c8f580a9b00.png) Αντικαθιστω οπου
Αντικαθιστω οπου  στο τριωνυμο και παιρνω
στο τριωνυμο και παιρνω  που ειναι δεκτη λυση για τo
που ειναι δεκτη λυση για τo 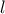 αφου ειναι
αφου ειναι  που ισχυει
που ισχυει 
 μας μενει μονο η συναληθευση με την ανισωση του πρωτου ερωτηματος . Γραφικα ευκολα φαινονται να συναληθευουν στο
μας μενει μονο η συναληθευση με την ανισωση του πρωτου ερωτηματος . Γραφικα ευκολα φαινονται να συναληθευουν στο  .
.
 και
και 

 ανήκει στη γραφική παράσταση της
ανήκει στη γραφική παράσταση της 

 και η αλλη
και η αλλη  Συναληθεύουν στο
Συναληθεύουν στο 

 αρα εδειχθη
αρα εδειχθη  ευκολα η προς επιλυση εξισωση ειναι
ευκολα η προς επιλυση εξισωση ειναι  Βγαζω διακρινουσα στο τριωνυμο και ειναι
Βγαζω διακρινουσα στο τριωνυμο και ειναι  αρα ειναι
αρα ειναι  με την δευτερη λυση να αποριπτεται αφου δεν ανηκει στο πεδιο ορισμου .
με την δευτερη λυση να αποριπτεται αφου δεν ανηκει στο πεδιο ορισμου .
 του τριωνύμου και να λύσετε την εξίσωση
του τριωνύμου και να λύσετε την εξίσωση 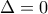



 που συναληθευουν στο
που συναληθευουν στο 


![6-3l+2l-7| \leq 21 \Leftrightarrow |l+1| \leq 21 \Leftrightarrow l \in [-22,20] 6-3l+2l-7| \leq 21 \Leftrightarrow |l+1| \leq 21 \Leftrightarrow l \in [-22,20]](/forum/ext/geomar/texintegr/latexrender/pictures/42f803433a3b95e9a829455be1d20f02.png) που συναληθευουν με την
που συναληθευουν με την  στο
στο ![l \in [-22,4) \cup (8,20] l \in [-22,4) \cup (8,20]](/forum/ext/geomar/texintegr/latexrender/pictures/7f85da90e5972c017821a83c912bd05b.png)
 που ειναι δεκτη .
που ειναι δεκτη . ισχύει η σχέση
ισχύει η σχέση 

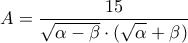 σε ισοδύναμο με ρητό παρονομαστή.
σε ισοδύναμο με ρητό παρονομαστή.
![\displaystyle{\Delta = \sqrt {\alpha \sqrt[3]{\alpha }} \cdot \sqrt[3]{\alpha } - \beta } \displaystyle{\Delta = \sqrt {\alpha \sqrt[3]{\alpha }} \cdot \sqrt[3]{\alpha } - \beta }](/forum/ext/geomar/texintegr/latexrender/pictures/180210baddf3c406f9015bb8c431a1fb.png)

 και
και  το άθροισμα και το γινόμενο αντίστοιχα των ριζών της εξίσωσης
το άθροισμα και το γινόμενο αντίστοιχα των ριζών της εξίσωσης  , να προσδιορίσετε την τιμή του
, να προσδιορίσετε την τιμή του 
 και
και 


 το
το  αποριπτεται αφου η αριστερη ποσοτητα ειναι μεγαλυτερη απο την δεξια .
αποριπτεται αφου η αριστερη ποσοτητα ειναι μεγαλυτερη απο την δεξια . ![\displaystyle{ \Leftrightarrow D=\sqrt{\sqrt[3]{2^4}} \cdot \sqrt[3]{2}+3 \Leftrightarrow D=2+3=5 } \displaystyle{ \Leftrightarrow D=\sqrt{\sqrt[3]{2^4}} \cdot \sqrt[3]{2}+3 \Leftrightarrow D=2+3=5 }](/forum/ext/geomar/texintegr/latexrender/pictures/e9d1a8e20da67744aa09f545407e1807.png)

 Η δευτερη δεκτη η πρωτη αποριπτεται λογω περιοσμων που εχουν τεθει στο α ερωτημα .
Η δευτερη δεκτη η πρωτη αποριπτεται λογω περιοσμων που εχουν τεθει στο α ερωτημα . 
 αρα ειναι η
αρα ειναι η 
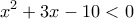
 που βρήκατε στο α) ερώτημα να υπολογίσετε την τιμή της παράστασης
που βρήκατε στο α) ερώτημα να υπολογίσετε την τιμή της παράστασης 
 που βρήκατε στο β) ερώτημα να υπολογίσετε την παράσταση
που βρήκατε στο β) ερώτημα να υπολογίσετε την παράσταση ![\displaystyle{B = \sqrt[3]{{3 + \sqrt[4]{{a + 1}}}} \cdot \sqrt[3]{{3 - \sqrt[4]{{a + 1}}}} \cdot \sqrt[3]{2}} \displaystyle{B = \sqrt[3]{{3 + \sqrt[4]{{a + 1}}}} \cdot \sqrt[3]{{3 - \sqrt[4]{{a + 1}}}} \cdot \sqrt[3]{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/28754ecce3c1c86af8b58fbcd9b9f937.png)

 της συνάρτησης
της συνάρτησης  ισχύει
ισχύει 


 αρα
αρα 

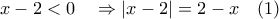


 γινεται :
γινεται :
![\displaystyle{ B=\sqrt[3]{3+\sqrt{5}} \cdot \sqrt[3]{3-\sqrt{5}} \cdot \sqrt[3]{2} \Leftrightarrow B=\sqrt[3}{2^2} \cdot \sqrt[3]{2} \Leftrightarrow B=\sqrt[3]{2^3}=2 } \displaystyle{ B=\sqrt[3]{3+\sqrt{5}} \cdot \sqrt[3]{3-\sqrt{5}} \cdot \sqrt[3]{2} \Leftrightarrow B=\sqrt[3}{2^2} \cdot \sqrt[3]{2} \Leftrightarrow B=\sqrt[3]{2^3}=2 }](/forum/ext/geomar/texintegr/latexrender/pictures/4024a7a0373da86b950401662551e84a.png)

 που ισχυει για καθε
που ισχυει για καθε 
 για καθε
για καθε  τοτε η ποσοτητα στο απολυτο ειναι αρνητικη αρα θα ειναι :
τοτε η ποσοτητα στο απολυτο ειναι αρνητικη αρα θα ειναι :
 Η οποια αληθευει για καθε
Η οποια αληθευει για καθε 

![(x-3)(x-1)(x)(x-6) \leq -5(x-1)(x-3) \Leftrightarrow (x-3)(x-1)[x^2-5x-x+5] \leq 0 \Leftrightarrow (x-1)(x-3)(x-1)(x-5) \leq 0 \Leftrightarrow (x-1)^2(x-3)(x-5) \leq 0 } (x-3)(x-1)(x)(x-6) \leq -5(x-1)(x-3) \Leftrightarrow (x-3)(x-1)[x^2-5x-x+5] \leq 0 \Leftrightarrow (x-1)(x-3)(x-1)(x-5) \leq 0 \Leftrightarrow (x-1)^2(x-3)(x-5) \leq 0 }](/forum/ext/geomar/texintegr/latexrender/pictures/703ba272aa62a6749ac4379cac907a61.png) από εδώ με ένα πινακάκι προκύπτει ότι
από εδώ με ένα πινακάκι προκύπτει ότι ![\displaystyle{ x \in [3,5]\cup \left\{ 1 \right\} \displaystyle{ x \in [3,5]\cup \left\{ 1 \right\}](/forum/ext/geomar/texintegr/latexrender/pictures/6a07d78b538728f3e17ae4f91d1f8297.png)


 να δείξετε οτι η εξίσωση
να δείξετε οτι η εξίσωση  για τις οποίες ισχύει
για τις οποίες ισχύει 

 αρα
αρα 
 Απαιτώ
Απαιτώ  Αρα για
Αρα για  έχει θετική διακρίνουσα αρα και δύο ανισες ρίζες
έχει θετική διακρίνουσα αρα και δύο ανισες ρίζες  Απο την εξίσωση μου θα πάρω ευκολα
Απο την εξίσωση μου θα πάρω ευκολα 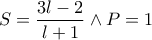 άρα θα είναι
άρα θα είναι 


 στην
στην  η διακρίνουσα της οποίας είναι η:
η διακρίνουσα της οποίας είναι η:  και τελικά οι λύσεις της:
και τελικά οι λύσεις της:  και:
και:  .
.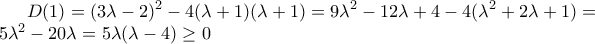 το οποίο προφανώς μηδενίζεται για
το οποίο προφανώς μηδενίζεται για  και θετικές για
και θετικές για  .
. .Η σχέση που μας δίνετε να βρούμε γράφετε και έτσι:
.Η σχέση που μας δίνετε να βρούμε γράφετε και έτσι:  .Έγινε διόρθωση.Ευχαριστώ τον Κύριο ΚΑΤΣΙΠΟΔΑ για τα ΠΜ του.
.Έγινε διόρθωση.Ευχαριστώ τον Κύριο ΚΑΤΣΙΠΟΔΑ για τα ΠΜ του.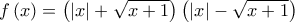

 έχει δύο ρίζες ετερόσημες τις οποίες και να υπολογίσετε.
έχει δύο ρίζες ετερόσημες τις οποίες και να υπολογίσετε.  ,όπου x ανήκει στο πεδίο ορισμού της συνάρτησης f.
,όπου x ανήκει στο πεδίο ορισμού της συνάρτησης f.  οι λύσεις της εξίσωσης του ερωτήματος Δ2, να υπολογίσετε τις τιμές των παρακάτω παραστάσεων
οι λύσεις της εξίσωσης του ερωτήματος Δ2, να υπολογίσετε τις τιμές των παρακάτω παραστάσεων
![\displaystyle\frac{1}{{\sqrt[{4024}]{A} - 3}} + \frac{1}{{\sqrt[{4024}]{A} + 3}} \displaystyle\frac{1}{{\sqrt[{4024}]{A} - 3}} + \frac{1}{{\sqrt[{4024}]{A} + 3}}](/forum/ext/geomar/texintegr/latexrender/pictures/7130575a7a28c765956b19243070861e.png)
 Με διαφορα τετραγώνων ευκολα καταληγω στο οτι
Με διαφορα τετραγώνων ευκολα καταληγω στο οτι 
 άρα δυο ρίζες και ανισες με
άρα δυο ρίζες και ανισες με 
 θέτω
θέτω  παίρνω
παίρνω  απόριψη της δευτερης και έχω
απόριψη της δευτερης και έχω 


![\begin{array}{l}
A = {\left( {2\sqrt 2 + \sqrt 2 {x_1}} \right)^{2012}} \cdot {\left( {2\sqrt 2 + \sqrt 2 {x_2}} \right)^{2012}} \\
\\
= {\left[ {\left( {2\sqrt 2 + \sqrt 2 {x_1}} \right)\left( {2\sqrt 2 + \sqrt 2 {x_2}} \right)} \right]^{2012}} \\
\\
= {\left( {8 + 4{x_1} + 4{x_2} + 2{x_1}{x_2}} \right)^{2012}} \\
\\
= {\left[ {8 + 4\left( {{x_1} + {x_2}} \right) + 2{x_1}{x_2}} \right]^{2012}} \\
\\
= {\left( {8 + 4 \cdot 1 - 2} \right)^{2012}} \\
\\
= {10^{2012}} \\
\end{array} \begin{array}{l}
A = {\left( {2\sqrt 2 + \sqrt 2 {x_1}} \right)^{2012}} \cdot {\left( {2\sqrt 2 + \sqrt 2 {x_2}} \right)^{2012}} \\
\\
= {\left[ {\left( {2\sqrt 2 + \sqrt 2 {x_1}} \right)\left( {2\sqrt 2 + \sqrt 2 {x_2}} \right)} \right]^{2012}} \\
\\
= {\left( {8 + 4{x_1} + 4{x_2} + 2{x_1}{x_2}} \right)^{2012}} \\
\\
= {\left[ {8 + 4\left( {{x_1} + {x_2}} \right) + 2{x_1}{x_2}} \right]^{2012}} \\
\\
= {\left( {8 + 4 \cdot 1 - 2} \right)^{2012}} \\
\\
= {10^{2012}} \\
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/ce31f3b11dfb7f6c0a329ae898be954e.png)
 , αν ισχύει
, αν ισχύει 