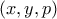 όπου
όπου  θετικοί ακέραιοι και
θετικοί ακέραιοι και  πρώτος, για τις οποίες ισχύει:
πρώτος, για τις οποίες ισχύει: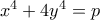
Έως 30 Νοεμβρίου - Άλγεβρα-Θεωρία Αριθμών Juniors
Συντονιστής: polysot
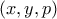 όπου
όπου  θετικοί ακέραιοι και
θετικοί ακέραιοι και  πρώτος, για τις οποίες ισχύει:
πρώτος, για τις οποίες ισχύει: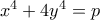
 .
. πρώτος, πρέπει
πρώτος, πρέπει  ή
ή  .
. .
. , με διακρίνουσα
, με διακρίνουσα  , άρα
, άρα  και
και  .
. .
.
 πρωτο.
πρωτο.Γεια σου Χάρη!ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Επειδη με πρόλαβε ο Ορεστης ας θέσω ενα ωραίο θεμα πανω στην ταυτότητα Sophie Germain.
Να λυθεί στους ακεραίους η εξισωση:

μεπρωτο.
 .
. .
.  .
. . Μπορούμε λοιπόν να θέσουμε
. Μπορούμε λοιπόν να θέσουμε  .
. .
. .
. , με Διακρίνουσα
, με Διακρίνουσα  .
. , το αριστερό μέλος της αρχικής είναι άρτιος, άρα
, το αριστερό μέλος της αρχικής είναι άρτιος, άρα  .
. , άτοπο.
, άτοπο. .
.Πρόκειται για το 2ο πρόβλημα στον Αρχιμήδη των Μεγάλων το σχολικό έτος 2007 - 2008. Δείτε κι εδώ.ΧΑΡΗΣ ΤΙΟΥΡΙΝΓΚ έγραψε:Επειδη με πρόλαβε ο Ορεστης ας θέσω ενα ωραίο θεμα πανω στην ταυτότητα Sophie Germain.
Να λυθεί στους ακεραίους η εξισωση:

μεπρωτο.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες