Πρόβλημα 1
Δίνονται δύο κύκλοι
 οι οποίοι τέμνονται στα
οι οποίοι τέμνονται στα  και
και  (με
(με  σημείο του
σημείο του 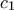
και
 σημείο του
σημείο του  ) η κοινή τους εφαπτομένη έτσι ώστε το
) η κοινή τους εφαπτομένη έτσι ώστε το  να βρίσκεται στο εσωτερικό του τριγώνου
να βρίσκεται στο εσωτερικό του τριγώνου  .
.Η
 τέμνει τον
τέμνει τον  στο
στο  και η
και η  τέμνει τον
τέμνει τον 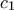 στο
στο  . Οι
. Οι  και
και  τέμνονται στο
τέμνονται στο  .
.Έστω
 η προβολή του
η προβολή του  πάνω στην
πάνω στην  . Θεωρούμε σημεία
. Θεωρούμε σημεία  πάνω στις
πάνω στις  αντιστοίχως έτσι ώστε
αντιστοίχως έτσι ώστε και
και  . Ο περιγεγραμμένος κύκλος (έστω
. Ο περιγεγραμμένος κύκλος (έστω  ) του τριγώνου
) του τριγώνου  τέμνει τις:
τέμνει τις:  στο
στο  ,
, στο
στο  και
και  στο
στο  . Αν οι
. Αν οι  τέμνουν τις
τέμνουν τις  αντίστοιχα στα
αντίστοιχα στα 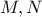 να αποδείξετε ότι τα
να αποδείξετε ότι τασημεία
 είναι ομοκυκλικά.
είναι ομοκυκλικά.Πρόβλημα 2
Να βρεθούν όλα τα πολυώνυμα
![P(x)\in\mathbb{Z}[x] P(x)\in\mathbb{Z}[x]](/forum/ext/geomar/texintegr/latexrender/pictures/8efbc35bbfe88264973589aa237c9dd1.png) (με ακέραιους συντελεστές) τα οποία ικανοποιούν την παρακάτω σχέση:
(με ακέραιους συντελεστές) τα οποία ικανοποιούν την παρακάτω σχέση:![(x-1)[(P(x+1)^2-P(x)]=xP(x^2)-1, \forall x\in\mathbb{R} (x-1)[(P(x+1)^2-P(x)]=xP(x^2)-1, \forall x\in\mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/6f86fed1bf4b9cc69c647de75d175d6d.png)
Πρόβλημα 3
Δίνεται το σύνολο
 το οποίο περιλαμβάνει όλους τους θετικούς ακεραίους. Ο μικρός Θανάσης έχει στην
το οποίο περιλαμβάνει όλους τους θετικούς ακεραίους. Ο μικρός Θανάσης έχει στηνδιάθεσή του 2 σημειωματάρια, ένα κόκκινο και ένα πράσινο. Σε κάθε κίνηση, ο Θανάσης επιλέγει έναν αριθμό από
το σύνολο
 (τον οποίο δεν έχει ξαναεπιλέξει προηγουμένως) και ψάχνει να βρει κατάλληλους θετικούς ακεραίους
(τον οποίο δεν έχει ξαναεπιλέξει προηγουμένως) και ψάχνει να βρει κατάλληλους θετικούς ακεραίους έτσι ώστε ο αριθμός που επέλεξε να είναι λύση της εξίσωσης
έτσι ώστε ο αριθμός που επέλεξε να είναι λύση της εξίσωσης  (δηλαδή αντικαθιστά
(δηλαδή αντικαθιστάτον αριθμό στην θέση του
 ). Αν υπάρχουν κατάλληλοι θετικοί ακέραιοι τότε σημειώνει τον αριθμό που επέλεξε στο
). Αν υπάρχουν κατάλληλοι θετικοί ακέραιοι τότε σημειώνει τον αριθμό που επέλεξε στοκόκκινο σημειωματάριο, διαφορετικά αν δεν υπάρχουν θετικοί ακέραιοι έτσι ώστε ο αριθμός που επέλεξε να είναι ρίζα,
τότε τον σημειώνει το πράσινο σημειωματάριο.
(α) Αν υποθέσουμε ότι ελέγχει όλους τους αριθμούς του
 , να αποδείξετε ότι υπάρχουν τουλάχιστον
, να αποδείξετε ότι υπάρχουν τουλάχιστον 
αριθμοί οι οποίοι θα γραφούν στο πράσινο σημειωματάριο.
(β) Να βρεθούν όλες οι δυνατές τιμές του θετικού ακέραιου
 για τον οποίο ισχύει ότι αν ο Θανάσης
για τον οποίο ισχύει ότι αν ο Θανάσηςδοκιμάσει όλους τους θετικούς ακέραιους από το
 μέχρι και το
μέχρι και το  στην θέση του
στην θέση του  στην παραπάνω
στην παραπάνωεξίσωση, τα δύο σημειωματάρια θα έχουν το ίδιο πλήθος αριθμών.
Πρόβλημα 4
Τετράγωνο
 πλευράς
πλευράς  όπου
όπου  θετικός ακέραιος διαιρείται σε
θετικός ακέραιος διαιρείται σε  μοναδιαία τετράγωνα όπως στο σχήμα. (Περίπτωση για
μοναδιαία τετράγωνα όπως στο σχήμα. (Περίπτωση για  ) Στην συνέχεια φέρνουμε την διαγώνιο του κάθε μοναδιαίου τετραγώνου που είναι παράλληλη με την
) Στην συνέχεια φέρνουμε την διαγώνιο του κάθε μοναδιαίου τετραγώνου που είναι παράλληλη με την  . Μία αράχνη ξεκινάει από το
. Μία αράχνη ξεκινάει από το  θέλοντας να φτάσει στο
θέλοντας να φτάσει στο  μέσω των ευθυγράμμων τμημάτων υπό τις εξής προϋποθέσεις:
μέσω των ευθυγράμμων τμημάτων υπό τις εξής προϋποθέσεις:1)Πρέπει να κινείται προς τα πάνω ή προς τα δεξιά
2)Μπορεί να διασχίσει ένα διαγώνιο ευθύγραμμο τμήμα από πάνω-αριστερά προς κάτω-δεξιά μήκους
 αν στην αμέσως προηγούμενη κίνηση κινήθηκε προς τα πάνω.
αν στην αμέσως προηγούμενη κίνηση κινήθηκε προς τα πάνω.Έστω
 το πλήθος των διαδρομών που μπορεί να διασχίσει η αράχνη για να φτάσει στο
το πλήθος των διαδρομών που μπορεί να διασχίσει η αράχνη για να φτάσει στο  από το
από το  . Να βρεθούν όλοι οι πρώτοι αριθμοί
. Να βρεθούν όλοι οι πρώτοι αριθμοί  που είναι τέτοιοι ώστε
που είναι τέτοιοι ώστε  Edit: Προσθήκη (β) ερωτήματος στο πρόβλημα 3
Edit: Προσθήκη (β) ερωτήματος στο πρόβλημα 3
 να είναι ισοσκελές.
να είναι ισοσκελές. , άρα πράγματι το
, άρα πράγματι το  , άρα τα τρίγωνα
, άρα τα τρίγωνα  και
και  είναι ορθογώνια, με άλλα λόγια τα
είναι ορθογώνια, με άλλα λόγια τα  και
και  του
του  το ορθόκεντρο του
το ορθόκεντρο του  και
και  αντίστοιχα.
αντίστοιχα.  , έχουμε τα ζεύγη μέσων
, έχουμε τα ζεύγη μέσων  και
και  . Συνεπώς έχουμε πως
. Συνεπώς έχουμε πως  και ότι
και ότι  . Όμως
. Όμως 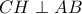 και
και  , άρα
, άρα  .
. είναι ομοκυκλικά (αφού το
είναι ομοκυκλικά (αφού το  είναι εγγράψιμο). Από την άλλη όμως είναι
είναι εγγράψιμο). Από την άλλη όμως είναι  (το
(το  είναι ομοκυκλικά (το
είναι ομοκυκλικά (το  είναι εγγράψιμο). Έπεται λοιπόν πως τα σημεία
είναι εγγράψιμο). Έπεται λοιπόν πως τα σημεία 
 ισοσκελές αφού
ισοσκελές αφού  και
και 
 Aρα
Aρα  και
και 
 (
( ισοσκελες , εγγεγραμένες τόξου
ισοσκελες , εγγεγραμένες τόξου  )
) (
( ισοσκελές , εγγεγραμένες τόξου
ισοσκελές , εγγεγραμένες τόξου  )
) ισοσκελή άρα
ισοσκελή άρα 

 καθετη
καθετη  καθετη
καθετη 



 εγγράψιμο
εγγράψιμο 
 ισοσκελές με
ισοσκελές με 
 επομένως
επομένως  ορθογώνιο τρίγωνο και
ορθογώνιο τρίγωνο και  καθετη
καθετη  ομοκυκλικά
ομοκυκλικά ώστε
ώστε  . Τότε
. Τότε  από το οποίο προκύπτει ότι
από το οποίο προκύπτει ότι  άρτιοι.
άρτιοι.  με τουλάχιστον έναν από τους
με τουλάχιστον έναν από τους  να είναι περιττός. Τότε
να είναι περιττός. Τότε![\displaystyle{ 2^{2k}[(r^2+s^2)x^n + rsx] = [2^k(r+s)]! \geqslant 2^{k+1}!} \displaystyle{ 2^{2k}[(r^2+s^2)x^n + rsx] = [2^k(r+s)]! \geqslant 2^{k+1}!}](/forum/ext/geomar/texintegr/latexrender/pictures/80a18832099d13be6170597f19e66929.png)
 που διαιρεί το αριστερό μέλος ισούται με
που διαιρεί το αριστερό μέλος ισούται με  . Η μεγαλύτερη δύναμη του
. Η μεγαλύτερη δύναμη του 
 στο πράσινο. Άρα μόνο για
στο πράσινο. Άρα μόνο για  θα έχουμε ίσους αριθμούς στα δυο σημειωματάρια αφού για
θα έχουμε ίσους αριθμούς στα δυο σημειωματάρια αφού για  με
με  θα έχουμε τουλάχιστον
θα έχουμε τουλάχιστον  αριθμούς στο πράσινο σημειωματάριο.
αριθμούς στο πράσινο σημειωματάριο. και
και  παρατηρούμε ότι ο
παρατηρούμε ότι ο  . Αν υπάρχουν τέτοια
. Αν υπάρχουν τέτοια  . Τότε
. Τότε 
 οπότε
οπότε  .
. . Άρα
. Άρα  . Παίρνουμε
. Παίρνουμε  . Επειδή το
. Επειδή το  δεν είναι τέλειο τετράγωνο
δεν είναι τέλειο τετράγωνο  πρέπει
πρέπει  .
. με τουλάχιστον ένα από τα
με τουλάχιστον ένα από τα  . Τότε
. Τότε![\displaystyle{ 5^{2k}[(r^2+s^2)x^n + rsx] = [5^k(r+s)]! \geqslant 2 \cdot 5^k} \displaystyle{ 5^{2k}[(r^2+s^2)x^n + rsx] = [5^k(r+s)]! \geqslant 2 \cdot 5^k}](/forum/ext/geomar/texintegr/latexrender/pictures/fd91b231ef5c5f510bdfe73c2036b42e.png)

 . Πρέπει επίσης
. Πρέπει επίσης  αφού σε αντίθετη περίπτωση η μεγαλύτερη δύναμη που διαιρεί το
αφού σε αντίθετη περίπτωση η μεγαλύτερη δύναμη που διαιρεί το ![[5^k(r+s)]! [5^k(r+s)]!](/forum/ext/geomar/texintegr/latexrender/pictures/36ac149178de689016080243eb0b5689.png) είναι τουλάχιστον
είναι τουλάχιστον  .
. . Άρα
. Άρα  . Τότε
. Τότε  . Αυτό όμως είναι αδύνατο
. Αυτό όμως είναι αδύνατο  αφού τα
αφού τα  και
και  είναι πολλαπλάσια του
είναι πολλαπλάσια του  ενώ το
ενώ το  όχι.
όχι. έχει βαθμό
έχει βαθμό  και έστω ότι
και έστω ότι 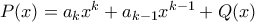 με το
με το  να έχει βαθμό το πολύ
να έχει βαθμό το πολύ  .
.![\displaystyle{ (x-1)[(P(x+1)^2-P(x)] = \cdots = a_k^2x^{2k+1} + [2a_k(ka_k + a_{k-1}) - a_k^2]x^{2k} + R_1(x)} \displaystyle{ (x-1)[(P(x+1)^2-P(x)] = \cdots = a_k^2x^{2k+1} + [2a_k(ka_k + a_{k-1}) - a_k^2]x^{2k} + R_1(x)}](/forum/ext/geomar/texintegr/latexrender/pictures/aada1b7e789ff240afdc8e4cb22f2059.png)

 είναι πολυώνυμα βαθμού το πολύ
είναι πολυώνυμα βαθμού το πολύ  .
.  και
και  με
με  . Η πρώτη εξίσωση δίνει
. Η πρώτη εξίσωση δίνει  . Μετά όμως η δεύτερη δίνει
. Μετά όμως η δεύτερη δίνει  , άτοπο.
, άτοπο. παίρνω
παίρνω  . Τώρα θέτοντας
. Τώρα θέτοντας  παίρνω
παίρνω  . Άρα το
. Άρα το 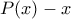 είναι ένα πολυώνυμο βαθμού το πολύ
είναι ένα πολυώνυμο βαθμού το πολύ  .
.