Γιάννης Μπόρμπας έγραψε: ↑Τρί Μάιος 02, 2017 3:49 pm
Διαγώνισμα 7 Επίπεδο: Αρχιμήδης/Προκριματικός Juniors
Πρόβλημα 3
Δίνεται τρίγωνο

εγγεγραμμένο σε κύκλο

. Οι εφαπτόμενες του κύκλου που διέρχονται από τα

τέμνονται
στο

. Η

τέμνει την

στο

. Η

τέμνει τον περιγεγραμμένο κύκλο
του τριγώνου

στο

.
Αν

είναι η προβολή του

στην

και η

τέμνει τον
στο

, να αποδείξετε ότι τα σημεία

είναι συνευθειακά.

- Προετοιμασία για διαγωνισμούς - Διαγ 7 - Πρ 3 - 1o μέρος.png (58.34 KiB) Προβλήθηκε 2247 φορές
Θεωρούμε για διευκόλυνση πως

είναι η τομή της

με τον κύκλο
. Πρέπει να αποδείξουμε πως τα σημεία

είναι συνευθειακά.
Έστω

το μέσο του

,

το σημείο τομής της

με τον

και

το σημείο τομής της

με τον
.
Έχουμε από δύναμη σημείου:

.
Θεωρούμε αντιστροφή με πόλο το

και δύναμη

(με άλλα λόγια κύκλος της αντιστροφής είναι ο κύκλος

).
Αρκεί να αποδείξουμε πως τα σημεία

είναι αντίστροφα σε αυτή την αντιστροφή.
Έπεται λοιπόν πως το

πηγαίνει στο

και το ανάποδο.
Ο περιγεγραμμένος κύκλος
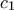
του

διέρχεται από το

(αφού

), που είναι ο πόλος της αντιστροφής, άρα γίνεται η ευθεία

.
Έπεται λοιπόν πως το

πηγαίνει στο

και το ανάποδο.
Το αντίστροφο λοιπόν του

είναι το

.
Επίσης το αντίστροφο του

είναι το σημείο τομής της

με τον περιγεγραμμένο κύκλο του

, έστω

.
Άρα το αντίστροφο του

είναι το σημείο τομής της

με τον περιγεγραμμένο κύκλο του

. Εμείς θέλουμε να αποδείξουμε πως αυτό το σημείο είναι το

, επομένως αρκεί το
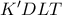
να είναι εγγράψιμο.
Αρκεί λοιπόν
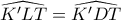
.
Όμως

, καθώς το

είναι εγγράψιμο.
Επομένως αρκεί

, δηλαδή αρκεί

.

- Προετοιμασία για διαγωνισμούς - Διαγ 7 - Πρ 3 - 2o μέρος.png (38.38 KiB) Προβλήθηκε 2247 φορές
Έστω

το σημείο τομής της

με την

και

το σημείο τομής της

με την προέκταση της

.
Αν αποδείξουμε πως το τρίγωνο

είναι ισοσκελές, τότε θα έχουμε πως το

είναι μέσο του

, άρα από την παραλληλία των

και

θα ισχύει πως
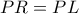
.
Είναι γνωστό πως η τετράδα

είναι αρμονική.
Επομένως η δέσμη

είναι αρμονική.
Άρα αφού
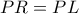
θα έχουμε από γνωστό λήμμα στις αρμονικές πως

, δηλαδή

που ήταν το ζητούμενο.
Αρκεί λοιπόν το τρίγωνο

να είναι ισοσκελές.
Έχουμε τώρα πως

, καθώς

, γιατί η

είναι συμμετροδιάμεσος του τριγώνου

.
Έχουμε τώρα πως

.
Εμείς θέλουμε να ισχύει ότι

.
Όμως έχουμε πως

, άρα

.
Έπεται λοιπόν πως θέλουμε να αποδείξουμε πως

.
Έστω

το μέσο του

.
Έχουμε τώρα πως

, επομένως αρκεί να αποδείξουμε πως
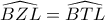
, δηλαδή ότι το

είναι εγγράψιμο.
Προεκτείνουμε την

και έστω πως τέμνει την

στο

.
Έχουμε πως

, άρα τα τρίγωνα

και

είναι όμοια. Επομένως έχουμε πως

.
Επομένως οι

και

είναι ισογώνιες στο τρίγωνο

.
Όμως το τετράπλευρο

είναι αρμονικό, αφού τα σημεία

είναι συνευθειακά. Άρα και το σημείο τομής των εφαπτομένων από τα

θα είναι πάνω στη διαγώνιο

. Άρα η συμμετροδιάμεσος του τριγώνου

στην κορυφή

είναι η

.
Έπεται λοιπόν πως η

είναι διάμεσος, άρα το

είναι μέσο του

.
Επομένως

και συνεπώς

.
Όμως λόγω του ότι οι

και

είναι ισογώνιες στο τρίγωνο

, έχουμε πως

.
Έπεται λοιπόν πως

και άρα το

είναι εγγράψιμο!!!
ΟΥΦ!
 που ικανοποιούν την παρακάτω εξίσωση:
που ικανοποιούν την παρακάτω εξίσωση:
 είναι θετικοί πραγματικοί αριθμοί με άθροισμα
είναι θετικοί πραγματικοί αριθμοί με άθροισμα  να βρεθεί η ελάχιστη τιμή της παράστασης:
να βρεθεί η ελάχιστη τιμή της παράστασης:
 εγγεγραμμένο σε κύκλο
εγγεγραμμένο σε κύκλο  . Οι εφαπτόμενες του κύκλου που διέρχονται από τα
. Οι εφαπτόμενες του κύκλου που διέρχονται από τα  τέμνονται
τέμνονται . Η
. Η  τέμνει την
τέμνει την  στο
στο  . Η
. Η  τέμνει τον περιγεγραμμένο κύκλο
τέμνει τον περιγεγραμμένο κύκλο 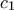 του τριγώνου
του τριγώνου  στο
στο  .
. είναι η προβολή του
είναι η προβολή του  στην
στην  και η
και η  τέμνει τον
τέμνει τον 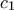 στο
στο  , να αποδείξετε ότι τα σημεία
, να αποδείξετε ότι τα σημεία  είναι συνευθειακά.
είναι συνευθειακά. αντίστοιχα η 1η, 2η, 3η, 4η στήλη).
αντίστοιχα η 1η, 2η, 3η, 4η στήλη). διαδοχικούς θετικούς ακέραιους στον πίνακα, (έστω
διαδοχικούς θετικούς ακέραιους στον πίνακα, (έστω 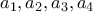 με
με  )
) να βρίσκεται στην
να βρίσκεται στην  στήλη. Σε κάθε κίνηση, ο Θανάσης μπορεί να επιλέξει
στήλη. Σε κάθε κίνηση, ο Θανάσης μπορεί να επιλέξει  αριθμούς
αριθμούς 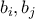 οι οποίοι
οι οποίοι 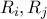 αντίστοιχα με
αντίστοιχα με  και
και  , να τους σβήσει, και από κάτω τους να γράψει τους
, να τους σβήσει, και από κάτω τους να γράψει τους  ή
ή  αντίστοιχα.
αντίστοιχα.  ο Θανάσης μπορεί να βρει
ο Θανάσης μπορεί να βρει  διαδοχικούς θετικούς ακέραιους μεγαλύτερους του
διαδοχικούς θετικούς ακέραιους μεγαλύτερους του  έτσι ώστε
έτσι ώστε συμβολίζουμε τον μέγιστο κοινό διαιρέτη των
συμβολίζουμε τον μέγιστο κοινό διαιρέτη των  .
.
 , τότε με
, τότε με  , πρέπει
, πρέπει  , άρα
, άρα  .
. , είναι
, είναι  , άρα
, άρα  , άτοπο.
, άτοπο. ή
ή  .
. , με λύση
, με λύση  .
.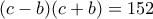 , με λύσεις
, με λύσεις  και
και  .
. .
. .
.  , ανν
, ανν  . (Εξήγηση: Αντικαθιστούμε όπου
. (Εξήγηση: Αντικαθιστούμε όπου  στους παρανομαστές και στους αριθμητές που έχουν την μορφή
στους παρανομαστές και στους αριθμητές που έχουν την μορφή 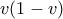 και εφαρμόζουμε την
και εφαρμόζουμε την  )
) 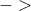

 , ανν
, ανν  με
με  περιττό, τότε μπορώ να τους κάνω
περιττό, τότε μπορώ να τους κάνω  ως εξής:
ως εξής:
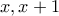

 και εφαρμόζοντας το πιο πάνω διαδοχικά (στις στήλες
και εφαρμόζοντας το πιο πάνω διαδοχικά (στις στήλες  και
και  . Μετά από ακόμη δυο βήματα καταλήγω στο
. Μετά από ακόμη δυο βήματα καταλήγω στο  .
. με τον κύκλο
με τον κύκλο  είναι συνευθειακά.
είναι συνευθειακά. το μέσο του
το μέσο του  το σημείο τομής της
το σημείο τομής της  και
και  το σημείο τομής της
το σημείο τομής της  .
. (με άλλα λόγια κύκλος της αντιστροφής είναι ο κύκλος
(με άλλα λόγια κύκλος της αντιστροφής είναι ο κύκλος  ).
). είναι αντίστροφα σε αυτή την αντιστροφή.
είναι αντίστροφα σε αυτή την αντιστροφή. ), που είναι ο πόλος της αντιστροφής, άρα γίνεται η ευθεία
), που είναι ο πόλος της αντιστροφής, άρα γίνεται η ευθεία  πηγαίνει στο
πηγαίνει στο  , έστω
, έστω  .
. . Εμείς θέλουμε να αποδείξουμε πως αυτό το σημείο είναι το
. Εμείς θέλουμε να αποδείξουμε πως αυτό το σημείο είναι το 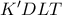 να είναι εγγράψιμο.
να είναι εγγράψιμο.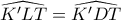 .
. , καθώς το
, καθώς το  είναι εγγράψιμο.
είναι εγγράψιμο. , δηλαδή αρκεί
, δηλαδή αρκεί  .
. το σημείο τομής της
το σημείο τομής της  με την
με την  και
και  το σημείο τομής της
το σημείο τομής της  .
. είναι ισοσκελές, τότε θα έχουμε πως το
είναι ισοσκελές, τότε θα έχουμε πως το  και
και  θα ισχύει πως
θα ισχύει πως 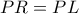 .
. είναι αρμονική.
είναι αρμονική. είναι αρμονική.
είναι αρμονική. , δηλαδή
, δηλαδή  , καθώς
, καθώς  , γιατί η
, γιατί η  είναι συμμετροδιάμεσος του τριγώνου
είναι συμμετροδιάμεσος του τριγώνου  .
. .
. , άρα
, άρα  .
. .
.  το μέσο του
το μέσο του  .
. , επομένως αρκεί να αποδείξουμε πως
, επομένως αρκεί να αποδείξουμε πως 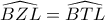 , δηλαδή ότι το
, δηλαδή ότι το  είναι εγγράψιμο.
είναι εγγράψιμο. και έστω πως τέμνει την
και έστω πως τέμνει την  στο
στο  .
. , άρα τα τρίγωνα
, άρα τα τρίγωνα  και
και  είναι όμοια. Επομένως έχουμε πως
είναι όμοια. Επομένως έχουμε πως  .
. είναι ισογώνιες στο τρίγωνο
είναι ισογώνιες στο τρίγωνο  .
. είναι αρμονικό, αφού τα σημεία
είναι αρμονικό, αφού τα σημεία  είναι συνευθειακά. Άρα και το σημείο τομής των εφαπτομένων από τα
είναι συνευθειακά. Άρα και το σημείο τομής των εφαπτομένων από τα  θα είναι πάνω στη διαγώνιο
θα είναι πάνω στη διαγώνιο  στην κορυφή
στην κορυφή  είναι η
είναι η  .
. και συνεπώς
και συνεπώς  .
. .
. και άρα το
και άρα το  τότε μπορούμε να δούμε (π.χ με κύκλο αντιστροφής τον
τότε μπορούμε να δούμε (π.χ με κύκλο αντιστροφής τον  ότι
ότι  ομοκυκλικά και έτσι
ομοκυκλικά και έτσι  οπότε αρκεί
οπότε αρκεί  .Επειδή
.Επειδή 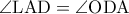 αρκεί
αρκεί  .Το
.Το  είναι το
είναι το  του
του 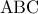 οπότε από γνωστή του ιδιότητα οι
οπότε από γνωστή του ιδιότητα οι  τέμνονται πάνω στην εφαπτομένη του
τέμνονται πάνω στην εφαπτομένη του  στο
στο  και
και  ,έτσι αν
,έτσι αν  είναι
είναι  και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε. είναι εγγράψιμο, διότι μετά το ζητούμενο έπεται από την τομή των ριζικών αξόνων και θα βγει το
είναι εγγράψιμο, διότι μετά το ζητούμενο έπεται από την τομή των ριζικών αξόνων και θα βγει το  η τομή της
η τομή της  με τον περίκυκλο του
με τον περίκυκλο του  , η δέσμη
, η δέσμη  είναι αρμονική. Όμως και η δέσμη
είναι αρμονική. Όμως και η δέσμη  είναι αρμονική, άρα
είναι αρμονική, άρα  συνευθειακά. Ακόμη
συνευθειακά. Ακόμη  και
και  αφού τα
αφού τα  είναι αντιδιαμετρικά στον περίκυλο του
είναι αντιδιαμετρικά στον περίκυλο του  . Άρα
. Άρα  . Όμως
. Όμως 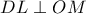 . Οπότε
. Οπότε  συνευθειακά. Παίρνω αντοστροφή
συνευθειακά. Παίρνω αντοστροφή  και:
και: μένουν εκεί που είναι. Το
μένουν εκεί που είναι. Το  , και το
, και το  εγγράψιμο. Παίρνω 2η αντίστροφη
εγγράψιμο. Παίρνω 2η αντίστροφη  και:
και: με την
με την  , όπου
, όπου  τα ίχνη των 2 άλλων υψών του
τα ίχνη των 2 άλλων υψών του  είναι το μέσο του
είναι το μέσο του 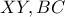 . Το
. Το  ,
,  δηλαδή στο αντίστροφο του
δηλαδή στο αντίστροφο του  , στην τομή της
, στην τομή της  να είναι συνευθειακά. Παίρνοντας σπειροειδή ομοιοθεσία με κέντρο
να είναι συνευθειακά. Παίρνοντας σπειροειδή ομοιοθεσία με κέντρο 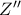 και το
και το 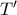 στο αντιδιαμετρικό του
στο αντιδιαμετρικό του  . Αρκεί
. Αρκεί  να είναι συνευθειακά (γνωστό, το αποδυκνείω για λόγους πληρότητας). To μέσο της
να είναι συνευθειακά (γνωστό, το αποδυκνείω για λόγους πληρότητας). To μέσο της  του εγγράψιμου
του εγγράψιμου  και άρα το κέντρο του περίκυκλου του
και άρα το κέντρο του περίκυκλου του