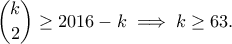Πρόβλημα 1
Να δείξετε ότι

για όλους τους πραγματικούς αριθμούς
 Για ποιες ακέραιες τιμές των
Για ποιες ακέραιες τιμές των  ισχύει η ισότητα;
ισχύει η ισότητα; Πρόβλημα 2
Θεωρούμε
 σημεία στο χώρο, ανά τέσσερα μη συνευθειακά. Να δείξετε ότι υπάρχουν
σημεία στο χώρο, ανά τέσσερα μη συνευθειακά. Να δείξετε ότι υπάρχουν  σημεία από αυτά, ανά τρία μη συνευθειακά.
σημεία από αυτά, ανά τρία μη συνευθειακά. Πρόβλημα 3
Να βρείτε όλα τα ζεύγη ακεραίων
 τέτοια, ώστε
τέτοια, ώστε 
Πρόβλημα 4
Έστω
 κυρτό τετράπλευρο τέτοιο ώστε
κυρτό τετράπλευρο τέτοιο ώστε  Οι ευθείες
Οι ευθείες  και
και  τέμνονται στο
τέμνονται στο  και οι περιγεγραμμένοι κύκλοι των τριγώνων
και οι περιγεγραμμένοι κύκλοι των τριγώνων  και
και 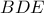 στα σημεία
στα σημεία  και
και  Αν
Αν  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  και
και  να δείξετε ότι η ευθεία
να δείξετε ότι η ευθεία  διχοτομεί τη γωνία
διχοτομεί τη γωνία 

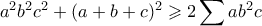 , που γράφεται
, που γράφεται  , που ισχύει.
, που ισχύει. (μία οικογένεια λύσεων για
(μία οικογένεια λύσεων για  είναι η
είναι η  (
( )).
)).
 ζυγός και έστω
ζυγός και έστω  .Στη συνέχεια θα δείξουμε ότι
.Στη συνέχεια θα δείξουμε ότι  πρέπει να είναι ζυγός.
πρέπει να είναι ζυγός. , εδώ παρατηρούμε ότι αν
, εδώ παρατηρούμε ότι αν  τότε
τότε  και
και  άτοπο.
άτοπο. και άρα
και άρα 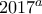 mod64)
mod64) της αρχικής εξίσωσης(!) είναι τέλειο τετράγωνο και άρα και το
της αρχικής εξίσωσης(!) είναι τέλειο τετράγωνο και άρα και το  θα πρέπει να είναι.
θα πρέπει να είναι. ισχύει
ισχύει  .Άρα έχουμε τις περιπτώσεις
.Άρα έχουμε τις περιπτώσεις 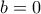 ή
ή  ή
ή  , από τις οποίες η μόνη που δίνει λύση είναι για
, από τις οποίες η μόνη που δίνει λύση είναι για  .Τέλος έχουμε και την προφανή λύση
.Τέλος έχουμε και την προφανή λύση  .
. .
. που τέμνει τον περίκυκλο του
που τέμνει τον περίκυκλο του  στο
στο  . Τότε
. Τότε  συντρέχουν στο ριζικό κέντρο των κύκλων που είναι το
συντρέχουν στο ριζικό κέντρο των κύκλων που είναι το  είναι συνευθειακά. Αφού
είναι συνευθειακά. Αφού  τότε αν αποδείξω ότι
τότε αν αποδείξω ότι  από νόμο ημιτόνων έχω το ζητούμενο. Αν όμως
από νόμο ημιτόνων έχω το ζητούμενο. Αν όμως  .
.  ,
,  και
και  .
. ως προσκείμενες στη βάση ισοσκελούς και με angle-chasing από τα εγγράψιμα παίρνω τις ισότητες:
ως προσκείμενες στη βάση ισοσκελούς και με angle-chasing από τα εγγράψιμα παίρνω τις ισότητες: 

 είναι εγγράψιμο αφού
είναι εγγράψιμο αφού  αφού η
αφού η είναι εξωτερική γωνία του τριγώνου
είναι εξωτερική γωνία του τριγώνου  , άρα
, άρα  .
. και
και 
 και άρα
και άρα  και το ζητούμενο έπεται.
και το ζητούμενο έπεται. είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου 
 το μέγιστο πλήθος σημείων που είναι ανά 3 μη συνευθειακά. Αυτά ορίζουν ακριβώς
το μέγιστο πλήθος σημείων που είναι ανά 3 μη συνευθειακά. Αυτά ορίζουν ακριβώς  ευθείες.
ευθείες.  σημεία θα ανήκει αναγκαστικά σε μία από αυτές τις ευθείες.
σημεία θα ανήκει αναγκαστικά σε μία από αυτές τις ευθείες.