Πρόβλημα 1
Να δείξετε ότι

για όλους τους πραγματικούς αριθμούς
 με
με  Για ποιες ακέραιες τιμές των
Για ποιες ακέραιες τιμές των  ισχύει η ισότητα;
ισχύει η ισότητα; Πρόβλημα 2
Θεωρούμε τρίγωνο
 με
με  και
και  σημείο στο εσωτερικό του. Έστω
σημείο στο εσωτερικό του. Έστω  και
και  τα συμμετρικα του
τα συμμετρικα του  ως προς τις πλευρές
ως προς τις πλευρές 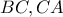 και
και  αντίστοιχα. Αν το τρίγωνο
αντίστοιχα. Αν το τρίγωνο  είναι ισόπλευρο, να δείξετε ότι η γωνία
είναι ισόπλευρο, να δείξετε ότι η γωνία  είναι ορθή.
είναι ορθή. Πρόβλημα 3
Να βρείτε όλες τις τριάδες πρώτων αριθμών
 για τις οποίες ισχύει
για τις οποίες ισχύει  και
και 
Πρόβλημα 4
Είκοσι παιδιά κρατούν
 σχοινιά. Τα άκρα κάθε σχοινιού κρατούν δύο παιδιά, ένα για κάθε άκρο. Δύο παιδιά μπορούν να κρατούν ένα μόνο κοινό σχοινί. Υποθέτουμε ότι ένα ζευγάρι σχοινιών των οποίων τα τέσσερα άκρα κρατούν διαφορετικά παιδιά μπορεί να επιλεγεί με ακριβώς
σχοινιά. Τα άκρα κάθε σχοινιού κρατούν δύο παιδιά, ένα για κάθε άκρο. Δύο παιδιά μπορούν να κρατούν ένα μόνο κοινό σχοινί. Υποθέτουμε ότι ένα ζευγάρι σχοινιών των οποίων τα τέσσερα άκρα κρατούν διαφορετικά παιδιά μπορεί να επιλεγεί με ακριβώς  τρόπους. Να αποδείξετε ότι κάθε παιδί κρατά τον ίδιο αριθμό σχοινιών.
τρόπους. Να αποδείξετε ότι κάθε παιδί κρατά τον ίδιο αριθμό σχοινιών.
 είναι
είναι  . Εύκολα έχουμε την λύση
. Εύκολα έχουμε την λύση  .
. .
. .
. , άτοπο.
, άτοπο. .
. , τότε
, τότε  (1).
(1). , άτοπο (το
, άτοπο (το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο  ).
). ,
,  , οπότε
, οπότε  (2).
(2). (3).
(3). , το οποίο με δοκιμές είναι αδύνατο.
, το οποίο με δοκιμές είναι αδύνατο. , άρα
, άρα  .
. , που μετά από πράξεις γράφεται
, που μετά από πράξεις γράφεται  , που ισχύει.
, που ισχύει. .
. )
) τα σημεία όπου οι
τα σημεία όπου οι  τέμνουν τις
τέμνουν τις  αντίστοιχα.
αντίστοιχα. , η
, η  ενώνει τα μέσα δύο πλευρών του, άρα
ενώνει τα μέσα δύο πλευρών του, άρα  , και όμοια
, και όμοια  .
. έχουν παράλληλες πλευρές, άρα είναι όμοια, οπότε
έχουν παράλληλες πλευρές, άρα είναι όμοια, οπότε  ισόπλευρο.
ισόπλευρο. εγγράψιμο, οπότε
εγγράψιμο, οπότε  και
και  .
. , οπότε οι
, οπότε οι  είναι συμπληρωματικές.
είναι συμπληρωματικές. είναι εγγράψιμα (εύκολο), άρα
είναι εγγράψιμα (εύκολο), άρα  , οπότε
, οπότε  συμπληρωματικές, που ισοδυναμεί με το ζητούμενο.
συμπληρωματικές, που ισοδυναμεί με το ζητούμενο. οι μαθητές.Κάθε σχοινί ''ενώνει'' δύο μαθητές οπότε θα γράφω
οι μαθητές.Κάθε σχοινί ''ενώνει'' δύο μαθητές οπότε θα γράφω  αν οι
αν οι  ενώνονται με σχοινί.Θεωρώ τα σύνολα
ενώνονται με σχοινί.Θεωρώ τα σύνολα  δηλαδή για κάθε μαθητή το σύνολο των μαθητών με τους οποίους ενώνεται.Αν με
δηλαδή για κάθε μαθητή το σύνολο των μαθητών με τους οποίους ενώνεται.Αν με  συμβολίσω το πλήθος των στοιχείων του συνόλου
συμβολίσω το πλήθος των στοιχείων του συνόλου  τότε επειδή
τότε επειδή  θα είναι
θα είναι 
 .
. έχουμε
έχουμε  μαθητές και για κάποιον
μαθητές και για κάποιον  μένουν
μένουν  σχοινιά.
σχοινιά. δυνατές επιλογές.
δυνατές επιλογές. φορές ( π.χ το
φορές ( π.χ το  το έχουμε μετρήσει και ως
το έχουμε μετρήσει και ως ![\left [ (a_j,a_i),(a_k,a_l) \right ],\left [ (a_k,a_l),(a_j,a_i) \right ] ,\left [ \left [ (a_l,a_k),(a_j,a_i) \right ] \right ] \left [ (a_j,a_i),(a_k,a_l) \right ],\left [ (a_k,a_l),(a_j,a_i) \right ] ,\left [ \left [ (a_l,a_k),(a_j,a_i) \right ] \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b0f6e2d63af926e810f99f55721abc44.png) )
)

 κάθε
κάθε  εμφανίζεται
εμφανίζεται  φορές (αφού
φορές (αφού 



 σχοινιά.
σχοινιά.  και
και δηλαδή
δηλαδή 
 ισχύει η ισότητα...
ισχύει η ισότητα...