![\displaystyle{f(x)=\begin{cases}x^2+1,~~~~x\in[0,1]\\1+\sqrt{x+3},~x\in(1,6] \end{cases}} \displaystyle{f(x)=\begin{cases}x^2+1,~~~~x\in[0,1]\\1+\sqrt{x+3},~x\in(1,6] \end{cases}}](/forum/ext/geomar/texintegr/latexrender/pictures/e13648600a2f5939cd0c97abe632f478.png)
είναι "1-1" και να ορίσετε την αντίστροφή της.
(Γ Λυκείου - Μέχρι 2/8/17)
Συντονιστής: polysot
![\displaystyle{f(x)=\begin{cases}x^2+1,~~~~x\in[0,1]\\1+\sqrt{x+3},~x\in(1,6] \end{cases}} \displaystyle{f(x)=\begin{cases}x^2+1,~~~~x\in[0,1]\\1+\sqrt{x+3},~x\in(1,6] \end{cases}}](/forum/ext/geomar/texintegr/latexrender/pictures/e13648600a2f5939cd0c97abe632f478.png)
Προς το παρόν αφήνω τις γραφικές παραστάσεις και θα επανέλθω αν δεν απαντηθεί.Γιώργος Απόκης έγραψε:Να αποδείξετε ότι η συνάρτηση
είναι "1-1" και να ορίσετε την αντίστροφή της.
(Γ Λυκείου - Μέχρι 2/8/17)
Καλημέρα Γιώργο!Γιώργος Απόκης έγραψε:Να αποδείξετε ότι η συνάρτηση
είναι "1-1" και να ορίσετε την αντίστροφή της.
(Γ Λυκείου - Μέχρι 2/8/17)
![x_1,x_2\in[0,1], x_1,x_2\in[0,1],](/forum/ext/geomar/texintegr/latexrender/pictures/98529855da4e3207b1fc78767a105dfc.png) με
με  είναι
είναι  άρα είναι γνησίως αύξουσα και επειδή είναι
άρα είναι γνησίως αύξουσα και επειδή είναι ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) θα έχει σύνολο τιμών
θα έχει σύνολο τιμών ![[f(0), f(1)]=[1,2]. [f(0), f(1)]=[1,2].](/forum/ext/geomar/texintegr/latexrender/pictures/5373482e67b9f0ca3e195a78b6c70de2.png) Ομοίως αποδεικνύεται ότι η
Ομοίως αποδεικνύεται ότι η  είναι συνεχής
είναι συνεχής ![(1,6], (1,6],](/forum/ext/geomar/texintegr/latexrender/pictures/6bba6edba1f4d7b42dd4f149e01966a7.png) οπότε θα έχει σύνολο τιμών
οπότε θα έχει σύνολο τιμών ![\displaystyle{\left( {\mathop {\lim }\limits_{x \to {1^ + }} f(x),f(6)} \right] = (3,4]} \displaystyle{\left( {\mathop {\lim }\limits_{x \to {1^ + }} f(x),f(6)} \right] = (3,4]}](/forum/ext/geomar/texintegr/latexrender/pictures/bf17309f3d2847a9c43fe302a1f89e0e.png)
 είναι
είναι  σε καθένα από τα διαστήματα
σε καθένα από τα διαστήματα ![[0,1],(1,6], [0,1],(1,6],](/forum/ext/geomar/texintegr/latexrender/pictures/53a77661fdad3f77f94f4e7bbf185ca0.png) οπότε αντιστρέφεται και η αντίστροφη συνάρτηση θα έχει πεδίο ορισμού σε κάθε κλάδο, το αντίστοιχο σύνολο τιμών της
οπότε αντιστρέφεται και η αντίστροφη συνάρτηση θα έχει πεδίο ορισμού σε κάθε κλάδο, το αντίστοιχο σύνολο τιμών της  .
.![y=f(x), x\in[0,1]. y=f(x), x\in[0,1].](/forum/ext/geomar/texintegr/latexrender/pictures/68ad938b1612f9706008ed3870c0ffb7.png) Τότε
Τότε  και
και ![\displaystyle{{f^{ - 1}}(x) = \sqrt {x - 1} ,x \in [1,2]} \displaystyle{{f^{ - 1}}(x) = \sqrt {x - 1} ,x \in [1,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/71158346d9b652d038f68df9c04bd8bf.png)
![y=f(x), x\in(1,6]. y=f(x), x\in(1,6].](/forum/ext/geomar/texintegr/latexrender/pictures/500537fc9b09b4020db450ce5337daeb.png) Τότε
Τότε  και
και ![\displaystyle{{f^{ - 1}}(x) = {x^2} - 2x - 2,x \in (3,4]} \displaystyle{{f^{ - 1}}(x) = {x^2} - 2x - 2,x \in (3,4]}](/forum/ext/geomar/texintegr/latexrender/pictures/e638bcbc11d607b6f91ba430968d8029.png)
![\boxed{{f^{ - 1}}(x) = \left\{ \begin{array}{l}
\sqrt {x - 1,} x \in [1,2]\\
{x^2} - 2x - 2,x \in (3,4]
\end{array} \right.} \boxed{{f^{ - 1}}(x) = \left\{ \begin{array}{l}
\sqrt {x - 1,} x \in [1,2]\\
{x^2} - 2x - 2,x \in (3,4]
\end{array} \right.}](/forum/ext/geomar/texintegr/latexrender/pictures/3cdef8f1ae25d9630221622291fdb070.png)
![x_1,x_2 \in [0,1] x_1,x_2 \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/7fa09a10a9bdea6a7ba161ddbc26ffa5.png) με
με  .
. .
. .
. είναι 1-1 στο διάστημα
είναι 1-1 στο διάστημα ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) .
. είναι 1-1 στο διάστημα
είναι 1-1 στο διάστημα ![(1,6] (1,6]](/forum/ext/geomar/texintegr/latexrender/pictures/ce365fba0e88c4917927ce97a928f3bf.png) .
.![x_1 \in [0,1] x_1 \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/1d2c2670a2ff955f01ece6e11ed1d7c9.png) και ένα
και ένα ![x_2 \in (1,6] x_2 \in (1,6]](/forum/ext/geomar/texintegr/latexrender/pictures/5d51b95c03c1648b3e02840c3b2d7ffc.png) και θα αποδείξουμε ότι δεν μπορούμε να έχουμε
και θα αποδείξουμε ότι δεν μπορούμε να έχουμε  .
.
 , που είναι άτοπο.
, που είναι άτοπο. .
. είναι 1-1.
είναι 1-1.![f(x)=x^2+1, x \in [0,1] f(x)=x^2+1, x \in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/b4e582eab7c48a29b0879c96acd3a5c7.png) .
. και πρέπει
και πρέπει  .
.![\boxed{f^{-1}(x)=\sqrt{x-1}, \, \, x \in [1,2]} \boxed{f^{-1}(x)=\sqrt{x-1}, \, \, x \in [1,2]}](/forum/ext/geomar/texintegr/latexrender/pictures/aad04d5f51ca0e06ef3500be8219c8ce.png) .
.![f(x)=\sqrt{x-3}+1, x \in (1,6] f(x)=\sqrt{x-3}+1, x \in (1,6]](/forum/ext/geomar/texintegr/latexrender/pictures/5cdd9901d3bb954246acb05d58abb4ed.png) .
.
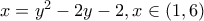 .
. .
.![\boxed{f^{-1}(x)=x^2-2x-2, \,\, x \in (3,4]} \boxed{f^{-1}(x)=x^2-2x-2, \,\, x \in (3,4]}](/forum/ext/geomar/texintegr/latexrender/pictures/2942e4d09d5a33d83dba81316f5882c1.png) .
.![\boxed{{f^{ - 1}}(x) = \left\{ \begin{array}{l}
\sqrt {x - 1,} \,\, x \in [1,2]\\
{x^2} - 2x - 2, \,\, x \in (3,4]
\end{array} \right.} \boxed{{f^{ - 1}}(x) = \left\{ \begin{array}{l}
\sqrt {x - 1,} \,\, x \in [1,2]\\
{x^2} - 2x - 2, \,\, x \in (3,4]
\end{array} \right.}](/forum/ext/geomar/texintegr/latexrender/pictures/6375be079230e8e7335f191e09a9bb83.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες