Γενικευμένο ολοκλήρωμα 9

#1

Ας υπολογισθεί το ακόλουθο ολοκλήρωμα:

$\displaystyle{\int_0^1\sqrt{4x-4x^2}\cdot\mathrm{tanh}^{-1}\left(\sqrt{4x-4x^2}\right)\,dx}$ .

#2

Κοτρώνης Αναστάσιος έγραψε:Ας υπολογισθεί το ακόλουθο ολοκλήρωμα: $\displaystyle{\int_0^1\sqrt{4x-4x^2}\cdot\mathrm{tanh}^{-1}\left(\sqrt{4x-4x^2}\right)\,dx}$ .

Κάπως συνοπτικά ..

$\displaystyle{\int\limits_0^1 {\sqrt {4x - 4{x^2}} \cdot {{\tanh }^{ - 1}}\left( {\sqrt {4x - 4{x^2}} } \right)dx} = 2\int\limits_0^{1/2} {\sqrt {4x - 4{x^2}} \cdot {{\tanh }^{ - 1}}\left( {\sqrt {4x - 4{x^2}} } \right)dx} = \mathop = \limits^{\sqrt {4x - 4{x^2}} = y} = }$

$\displaystyle{ = \int\limits_0^1 {\frac{{{y^2}}}{{\sqrt {1 - {y^2}} }} \cdot {{\tanh }^{ - 1}}\left( y \right)dy} = \frac{1}{2}\int\limits_0^1 {\frac{{{y^2}}}{{\sqrt {1 - {y^2}} }} \cdot \log \frac{{1 + y}}{{1 - y}}dy} = \mathop = \limits^{y = \cos x} = \frac{1}{2}\int\limits_0^{\pi /2} {{{\cos }^2}x \cdot \log \frac{{1 + \cos x}}{{1 - \cos x}}dx} = }$

$\displaystyle{ = \frac{1}{2}\int\limits_0^{\pi /2} {{{\cos }^2}x \cdot \left( {\log \left( {2{{\cos }^2}\frac{x}{2}} \right) - \log \left( {2{{\sin }^2}\frac{x}{2}} \right)} \right)dx} = \int\limits_0^{\pi /2} {{{\cos }^2}x \cdot \left( {\log \left( {\cos \frac{x}{2}} \right) - \log \left( {\sin \frac{x}{2}} \right)} \right)dx} = }$

$\displaystyle{ = \int\limits_0^{\pi /2} {{{\cos }^2}x \cdot \left( {\log \left( {2\cos \frac{x}{2}} \right) - \log \left( {2\sin \frac{x}{2}} \right)} \right)dx} = \int\limits_0^{\pi /2} {{{\cos }^2}x \cdot \left( {\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n - 1}}\cos nx}}{n}} + \sum\limits_{n = 1}^\infty {\frac{{\cos nx}}{n}} } \right)dx} = }$

$\displaystyle{ = 2\int\limits_0^{\pi /2} {{{\cos }^2}x\sum\limits_{n = 1}^\infty {\frac{{\cos \left( {2n - 1} \right)x}}{{2n - 1}}} \,dx} = 2\sum\limits_{n = 1}^\infty {\frac{1}{{2n - 1}}\int\limits_0^{\pi /2} {{{\cos }^2}x\cos \left( {2n - 1} \right)x\,dx} } = }$

$\displaystyle{ = \sum\limits_{n = 1}^\infty {\frac{1}{{2n - 1}}\int\limits_0^{\pi /2} {\left( {1 + \cos 2x} \right)\cos \left( {2n - 1} \right)x\,dx} } = \sum\limits_{n = 1}^\infty {\frac{1}{{2n - 1}}\left( {\frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{2n - 1}} + \frac{{{{\left( { - 1} \right)}^n}\left( {2n - 1} \right)}}{{\left( {2n + 1} \right)\left( {2n - 3} \right)}}} \right)} = }$

$\displaystyle{ = \sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{{\left( {2n - 1} \right)}^2}}}} + \sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{\left( {2n + 1} \right)\left( {2n - 3} \right)}}} = \sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{{\left( {2n - 1} \right)}^2}}}} + \frac{1}{4}\left( {\sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{2n - 3}}} - \sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{2n + 1}}} } \right) = }$

$\displaystyle{ = \sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n - 1}}}}{{{{\left( {2n - 1} \right)}^2}}}} + \frac{1}{4}\sum\limits_{n = 1}^2 {\frac{{{{\left( { - 1} \right)}^n}}}{{2n - 3}}} \Rightarrow \boxed{\int\limits_0^1 {\sqrt {4x - 4{x^2}} \cdot {{\tanh }^{ - 1}}\left( {\sqrt {4x - 4{x^2}} } \right)dx} = G + \frac{1}{2}}}$

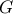όπου $\displaystyle{G}$ η σταθερά του Catalan και θεωρώντας γνωστό ότι $\displaystyle{\log \left( {2\sin \frac{x}{2}} \right) = - \sum\limits_{n = 1}^\infty {\frac{{\cos nx}}{n}} }$ και ότι $\displaystyle{\log \left( {2\cos \frac{x}{2}} \right) = \sum\limits_{n = 1}^\infty {\frac{{{{\left( { - 1} \right)}^{n - 1}}\cos nx}}{n}} }$

#3

Ωραία Σεραφείμ! Δυο ακόμα λύσεις εδώ σελ. 11-12.

Γενικευμένο ολοκλήρωμα 9

Γενικευμένο ολοκλήρωμα 9

Re: Γενικευμένο ολοκλήρωμα 9

Re: Γενικευμένο ολοκλήρωμα 9

Μέλη σε σύνδεση