Έχω την εξής σχέση:

πώς προκύπτει ότι το πρώτο ολοκλήρωμα είναι μηδέν λόγω του ότι η ολοκληρωτέα συνάρτηση είναι περιττή;
Ευχαριστώ για όποιον βοηθήσει.
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος

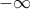 έως
έως  , οπότε μάλλον προκύπτει από τη συμμετρία που έχει η γραφική παράσταση μίας τέτοιας συνάρτησης και κατά συνέπεια από την ύπαρξη του ίδιου εμβαδού κάτω και πάνω από τον
, οπότε μάλλον προκύπτει από τη συμμετρία που έχει η γραφική παράσταση μίας τέτοιας συνάρτησης και κατά συνέπεια από την ύπαρξη του ίδιου εμβαδού κάτω και πάνω από τον  υποθέτω.
υποθέτω.Κώστα καλησπέρα!KostasA έγραψε:γνωρίζουμε ότι το ημίτονο είναι περιττή συνάρτηση άρα και συμμετρική ως προς την αρχή των αξόνων και το συνημίτονο άρτια, άρα κανονικά το δεύτερο ολοκλήρωμα δεν θα έπρεπε να είναι 0;
 περιττή αλλα
περιττή αλλα  άρτια
άρτια
 καί
καί  εύκολα αποδεικνύεται ότι συγκλίνουν.
εύκολα αποδεικνύεται ότι συγκλίνουν. τά πράγματα δέν είναι τόσο απλά:
τά πράγματα δέν είναι τόσο απλά: καί
καί  , τό
, τό 
 άρα καί τό
άρα καί τό 
 αποκλίνουν.
αποκλίνουν. , λόγω περιττότητας, είναι η πρωτεύουσα τιμή
, λόγω περιττότητας, είναι η πρωτεύουσα τιμή  τού
τού ![\displaystyle\int_{-\pi}^{\pi}{\frac{\cos({ax})}{bx}\,dx}=\lim_{\varepsilon\rightarrow 0+} \left[{\int_{-\pi}^{-\varepsilon} \frac{\cos({ax})}{bx}\,dx+\int_{\varepsilon}^{\pi}\frac{\cos({ax})}{bx}\,dx}\right] \displaystyle\int_{-\pi}^{\pi}{\frac{\cos({ax})}{bx}\,dx}=\lim_{\varepsilon\rightarrow 0+} \left[{\int_{-\pi}^{-\varepsilon} \frac{\cos({ax})}{bx}\,dx+\int_{\varepsilon}^{\pi}\frac{\cos({ax})}{bx}\,dx}\right]](/forum/ext/geomar/texintegr/latexrender/pictures/75bfa75e9598d52a989eb3eff10cd2d8.png) , άρα καί τού
, άρα καί τού 

![\frac{1}{T}\int_{t_{0}}^{t_{0}+T}{\cos\left[\left(n+m \right)\Omega _{0}t \right]dt}+ \frac{1}{T}\int_{t_{0}}^{t_{0}+T}{\cos\left[\left(n-m \right)\Omega _{0}t \right]dt}=\begin{cases}
0 & \text{ if } n\neq m \\
1 & \text{ if } n=m
\end{cases} \frac{1}{T}\int_{t_{0}}^{t_{0}+T}{\cos\left[\left(n+m \right)\Omega _{0}t \right]dt}+ \frac{1}{T}\int_{t_{0}}^{t_{0}+T}{\cos\left[\left(n-m \right)\Omega _{0}t \right]dt}=\begin{cases}
0 & \text{ if } n\neq m \\
1 & \text{ if } n=m
\end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/e45a4ba103252a83fd395a610001ce4c.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης