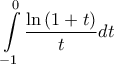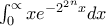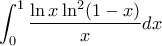Κοτρώνης Αναστάσιος έγραψε:Έστω
. Ας υπολογισθεί το
.
Γενικευμένα Ολοκληρώματα
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Όρια με ολοκληρώματα
- Συνημμένα
-
- Kotrw-4.jpg (57.02 KiB) Προβλήθηκε 5758 φορές
Σεραφείμ Τσιπέλης
-
kwstas12345
- Δημοσιεύσεις: 1052
- Εγγραφή: Δευ Ιαν 11, 2010 2:12 pm
Re: Γενικευμένα Ολοκληρώματα
11)Να αποδείξετε ότι το παρακάτω ολοκλήρωμα συγκλίνει:
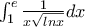
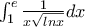
τελευταία επεξεργασία από kwstas12345 σε Τετ Ιουν 23, 2010 2:00 pm, έχει επεξεργασθεί 3 φορές συνολικά.
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Γενικευμένα Ολοκληρώματα
mathxl έγραψε:10) Να δείξετε ότι το ολοκλήρωμα
συγκλίνει
- Συνημμένα
-
- Kotrw-5.jpg (14.97 KiB) Προβλήθηκε 5759 φορές
Σεραφείμ Τσιπέλης
Re: Όρια με ολοκληρώματα
Με αλλαγη μεταβλητης σεΚοτρώνης Αναστάσιος έγραψε:Έστω
. Για
, ορίζουμε
.
Δείξτε ότιγια
.
 εχουμε
εχουμε 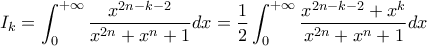 και απο ανισοτητα Jensen στην εκθετικη εχουμε
και απο ανισοτητα Jensen στην εκθετικη εχουμε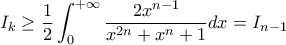
Δημητρης Σκουτερης
Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Γενικευμένα Ολοκληρώματα
Μάλλον κάποιο τυπογραφικό υπάρχει. Το ολοκλήρωμα συγκλίνει.kwstas12345 έγραψε:Να αποδείξετε ότι το παρακάτω ολοκλήρωμα αποκλίνει:
Είναι
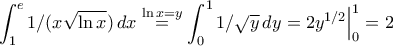 .
.*******************************************************************************************
Δίνω ένα κάπως παρόμοιο, λίγο πιο γενικό.
 Να μελετήσετε τη σύγκλιση του ολοκληρώματος
Να μελετήσετε τη σύγκλιση του ολοκληρώματος 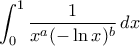 για τις διάφορες τιμές των
για τις διάφορες τιμές των  .
.Υ.Γ. : Κώστα αν θες αρίθμησε την άσκησή σου ως 11).
Εσύ....; Θα γίνεις κανίβαλος....;
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Γενικευμένα Ολοκληρώματα
Δίνω μερικά ακόμα :
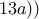 Ας υπολογιστεί το
Ας υπολογιστεί το 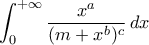 όπου
όπου 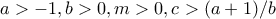
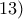 Ας υπολογιστεί το
Ας υπολογιστεί το 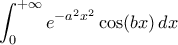 όπου
όπου 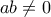 .
.
Και δυο μάλλον περισσότερο σάπια από όσο χρειάζεται..
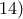
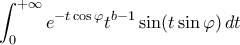 , όπου
, όπου 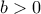 και
και 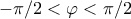 και
και
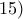
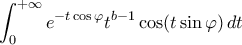 , όπου
, όπου 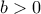 και
και 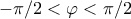 .
.
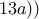 Ας υπολογιστεί το
Ας υπολογιστεί το 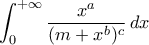 όπου
όπου 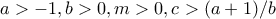
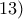 Ας υπολογιστεί το
Ας υπολογιστεί το 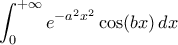 όπου
όπου 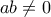 .
.Και δυο μάλλον περισσότερο σάπια από όσο χρειάζεται..
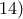
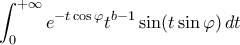 , όπου
, όπου 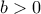 και
και 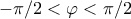 και
και 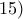
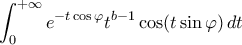 , όπου
, όπου 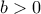 και
και 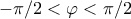 .
.
τελευταία επεξεργασία από Κοτρώνης Αναστάσιος σε Σάβ Ιουν 26, 2010 9:02 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Εσύ....; Θα γίνεις κανίβαλος....;
Re: Γενικευμένα Ολοκληρώματα
Ας πιασω το γρουσουζικο...Κοτρώνης Αναστάσιος έγραψε:Ας υπολογιστεί το
όπου
.
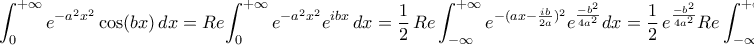
Αφου η συναρτηση δεν παρουσιαζει ανωμαλιες στο μιγαδικο επιπεδο, το ολοκληρωμα της 'μετατοπισμενης' Gaussian θα ισουται με αυτο της κανονικης, δηλαδη
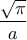 . Ετσι, το ολοκληρωμα μας ισουται με
. Ετσι, το ολοκληρωμα μας ισουται με 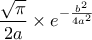 .
.Δημητρης Σκουτερης
Δημήτρης Σκουτέρης
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
Τα μαθηματικά είναι η μοναδική επιστήμη που θα μπορούσε κανείς να εξακολουθήσει να ασκεί αν κάποτε ξυπνούσε και το σύμπαν δεν υπήρχε πλέον.
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Γενικευμένα Ολοκληρώματα
Μια κατά το δυνατόν αναλυτική λύση: Επειδήmathxl έγραψε:10) Να δείξετε ότι το ολοκλήρωμα
συγκλίνει
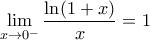 , έχουμε
, έχουμε 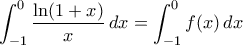 , όπου
, όπου 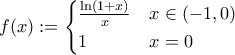 η οποία είναι συνεχής στο
η οποία είναι συνεχής στο ![\displaystyle{(-1,0]} \displaystyle{(-1,0]}](/forum/ext/geomar/texintegr/latexrender/pictures/57fc043f6480e31768e087df58fb0b24.png) με
με 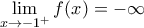 .
.Τώρα
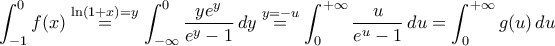 ,
, όπου
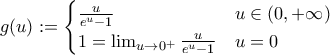 η οποία είναι συνεχής στο
η οποία είναι συνεχής στο  .
.Όμως για
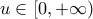 είναι
είναι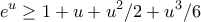 , αρα
, αρα 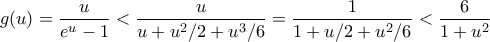 .
.Επειδή τώρα
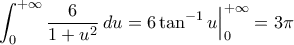 (συγκλίνει), συγκλίνει και το αρχικό ολοκλήρωμα.
(συγκλίνει), συγκλίνει και το αρχικό ολοκλήρωμα.Εσύ....; Θα γίνεις κανίβαλος....;
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Γενικευμένα Ολοκληρώματα
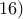 Ας εξετασθεί ως προς τη σύγκλιση το ολοκλήρωμα
Ας εξετασθεί ως προς τη σύγκλιση το ολοκλήρωμα 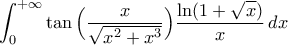 .
.Εσύ....; Θα γίνεις κανίβαλος....;
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Γενικευμένα Ολοκληρώματα
Κοτρώνης Αναστάσιος έγραψε:
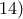
, όπου
και
και
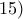
, όπου
και
.
- Συνημμένα
-
- Kotrw-6.jpg (47.87 KiB) Προβλήθηκε 5633 φορές
Σεραφείμ Τσιπέλης
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Γενικευμένα Ολοκληρώματα
Κοτρώνης Αναστάσιος έγραψε:
Ας υπολογιστεί το
όπου
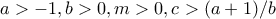
- Συνημμένα
-
- Kotrw-7.jpg (49.36 KiB) Προβλήθηκε 5633 φορές
Σεραφείμ Τσιπέλης
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Γενικευμένα Ολοκληρώματα
Κοτρώνης Αναστάσιος έγραψε:
Να μελετήσετε τη σύγκλιση του ολοκληρώματος
για τις διάφορες τιμές των
.
- Συνημμένα
-
- Kotrw-8.jpg (26.46 KiB) Προβλήθηκε 5617 φορές
Σεραφείμ Τσιπέλης
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Γενικευμένα Ολοκληρώματα
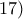 Σαν συνέχεια των ποστς
Σαν συνέχεια των ποστςviewtopic.php?f=9&t=7314
viewtopic.php?f=9&t=7877&p=46538#p46538 και
viewtopic.php?f=9&t=8239 ,
μια με θεωρητικό αλλά και πρακτικό ενδιαφέρον που αφορά τα ολολκληρώματα Frullani.
Για
 , ας υπολογισθεί το ολοκλήρωμα
, ας υπολογισθεί το ολοκλήρωμα 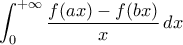 όπου η
όπου η  είναι συνεχής στο
είναι συνεχής στο  σε κάθε μια από τις παρακάτω περιπτώσεις:
σε κάθε μια από τις παρακάτω περιπτώσεις: Το ολοκλήρωμα
Το ολοκλήρωμα 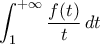 συγκλίνει,
συγκλίνει,
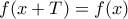 για κάποιο
για κάποιο 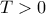 και για κάθε
και για κάθε 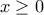 ,
,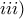
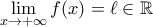 .
.
τελευταία επεξεργασία από Κοτρώνης Αναστάσιος σε Τρί Μαρ 08, 2011 11:59 am, έχει επεξεργασθεί 1 φορά συνολικά.
Εσύ....; Θα γίνεις κανίβαλος....;
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Γενικευμένα Ολοκληρώματα
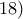 Δε θυμάμαι αν έχιυν ξανασυζητηθεί: Ας υπολογιστούν τα ολοκληρώματα
Δε θυμάμαι αν έχιυν ξανασυζητηθεί: Ας υπολογιστούν τα ολοκληρώματα
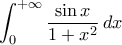

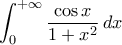 .
.(Με ή χωρίς μιγαδική ανάλυση. Θα προτιμούσα να δω κάποια λύση χωρίς πάντως..)
Εσύ....; Θα γίνεις κανίβαλος....;
Re: Γενικευμένα Ολοκληρώματα
18 β)

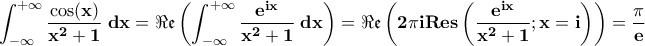 . Στην περίπτωσή μας θέλουμε το μισό του παραπάνω
. Στην περίπτωσή μας θέλουμε το μισό του παραπάνω
αποτελέσματος δηλαδή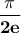 .
.

To α είναι λίγο δύσκολο....νομίζω αναφέρθηκε και πρόσφατα από τον mathxl.

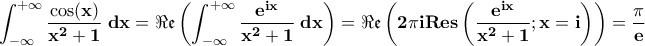 . Στην περίπτωσή μας θέλουμε το μισό του παραπάνω
. Στην περίπτωσή μας θέλουμε το μισό του παραπάνω αποτελέσματος δηλαδή
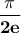 .
.
To α είναι λίγο δύσκολο....νομίζω αναφέρθηκε και πρόσφατα από τον mathxl.
What's wrong with a Greek in Hamburg?
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Γενικευμένα Ολοκληρώματα
Aναστάση θαρρώ πως αυτό μας είχε ξεφύγει (της προσοχής). Λοιπόν ...Κοτρώνης Αναστάσιος έγραψε:Ας υπολογισθεί το ολοκλήρωμα :
Έστω
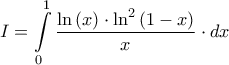
Θεωρούμε την συνάρτηση
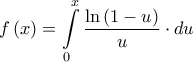 . Τότε :
. Τότε :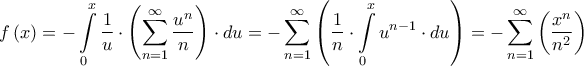 , που συγκλίνει για
, που συγκλίνει για 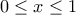
Επίσης ισχύουν
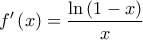 ,
,  και
και 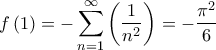 . Τότε
. Τότε ![\displaystyle{I = \int\limits_0^1 {f'\left( x \right) \cdot \ln \left( x \right) \cdot \ln \left( {1 - x} \right) \cdot dx} = \left[ {f\left( x \right) \cdot \ln \left( x \right) \cdot \ln \left( {1 - x} \right)} \right]_0^1 - \int\limits_0^1 {f\left( x \right) \cdot \left( {\dfrac{{\ln \left( {1 - x} \right)}}{x} - \dfrac{{\ln \left( x \right)}}{{1 - x}}} \right) \cdot dx} = } \displaystyle{I = \int\limits_0^1 {f'\left( x \right) \cdot \ln \left( x \right) \cdot \ln \left( {1 - x} \right) \cdot dx} = \left[ {f\left( x \right) \cdot \ln \left( x \right) \cdot \ln \left( {1 - x} \right)} \right]_0^1 - \int\limits_0^1 {f\left( x \right) \cdot \left( {\dfrac{{\ln \left( {1 - x} \right)}}{x} - \dfrac{{\ln \left( x \right)}}{{1 - x}}} \right) \cdot dx} = }](/forum/ext/geomar/texintegr/latexrender/pictures/7b5ded0a0dc6a589cc198f34e22ed127.png)
![\displaystyle{ = - \int\limits_0^1 {f\left( x \right) \cdot f'\left( x \right) \cdot dx} + \int\limits_0^1 {f\left( x \right) \cdot \dfrac{{\ln \left( x \right)}}{{1 - x}} \cdot dx} = - \frac{1}{2} \cdot \left[ {{f^2}\left( x \right)} \right]_0^1 + \int\limits_0^1 {f\left( x \right) \cdot \dfrac{{\ln \left( x \right)}}{{1 - x}} \cdot dx} =} \displaystyle{ = - \int\limits_0^1 {f\left( x \right) \cdot f'\left( x \right) \cdot dx} + \int\limits_0^1 {f\left( x \right) \cdot \dfrac{{\ln \left( x \right)}}{{1 - x}} \cdot dx} = - \frac{1}{2} \cdot \left[ {{f^2}\left( x \right)} \right]_0^1 + \int\limits_0^1 {f\left( x \right) \cdot \dfrac{{\ln \left( x \right)}}{{1 - x}} \cdot dx} =}](/forum/ext/geomar/texintegr/latexrender/pictures/1a2f65517a0e1518e697fc75cf36a1bb.png)
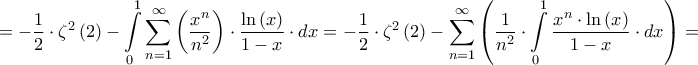
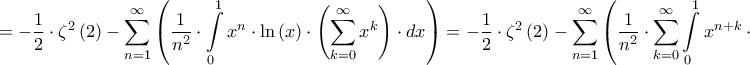
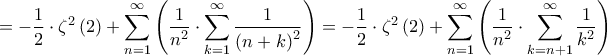
Όμως
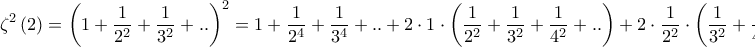
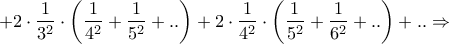
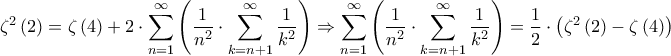
Οπότε
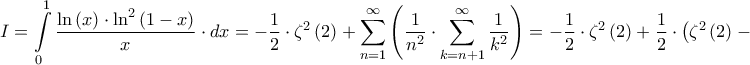
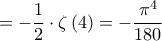
Σεραφείμ Τσιπέλης
- Σεραφείμ
- Επιμελητής
- Δημοσιεύσεις: 1872
- Εγγραφή: Τετ Μάιος 20, 2009 9:14 am
- Τοποθεσία: Θεσσαλονίκη - Γιάννενα
Re: Γενικευμένα Ολοκληρώματα
Χωρίς μιγαδική ανάλυση τα πράγματα δυσκολεύουν. Για την (β) θα χρησιμοποιηθούν κάποιες προηγμένες τεχνικές του μετασχηματισμού Laplace.Κοτρώνης Αναστάσιος έγραψε:Δε θυμάμαι αν έχιυν ξανασυζητηθεί: Ας υπολογιστούν τα ολοκληρώματα


.
(Με ή χωρίς μιγαδική ανάλυση. Θα προτιμούσα να δω κάποια λύση χωρίς πάντως..)
Ισχύει :
[1]
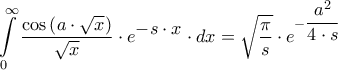 (Δ. Δασκαλόπουλος – Ανώτερα Μαθηματικά ΕΜΠ – Τόμος Τρίτος – σελ. 350-351) και
(Δ. Δασκαλόπουλος – Ανώτερα Μαθηματικά ΕΜΠ – Τόμος Τρίτος – σελ. 350-351) και[2]
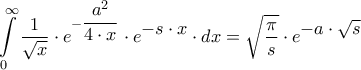 (Δ. Δασκαλόπουλος – Ανώτερα Μαθηματικά ΕΜΠ – Τόμος Τρίτος – σελ. 355-356)
(Δ. Δασκαλόπουλος – Ανώτερα Μαθηματικά ΕΜΠ – Τόμος Τρίτος – σελ. 355-356) Οπότε
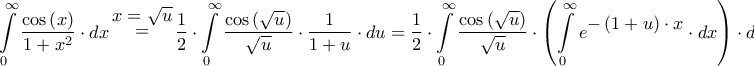
![\displaystyle{ = \dfrac{1}{2} \cdot \int\limits_0^\infty {{e^\big{{ - x}}} \cdot \left( {\int\limits_0^\infty {\dfrac{{\cos \left( {\sqrt u } \right)}}{{\sqrt u }} \cdot {e^\big{{ - u \cdot x}}} \cdot du} } \right) \cdot dx} \mathop = \limits^\big{{[1]}} \dfrac{1}{2} \cdot \int\limits_0^\infty {{e^\big{{ - x}}} \cdot \left( {\dfrac{{\sqrt \pi }}{{\sqrt x }} \cdot {e^{\dfrac{{ - 1}}{{4 \cdot x}}}}} \right) \cdot dx} = } \displaystyle{ = \dfrac{1}{2} \cdot \int\limits_0^\infty {{e^\big{{ - x}}} \cdot \left( {\int\limits_0^\infty {\dfrac{{\cos \left( {\sqrt u } \right)}}{{\sqrt u }} \cdot {e^\big{{ - u \cdot x}}} \cdot du} } \right) \cdot dx} \mathop = \limits^\big{{[1]}} \dfrac{1}{2} \cdot \int\limits_0^\infty {{e^\big{{ - x}}} \cdot \left( {\dfrac{{\sqrt \pi }}{{\sqrt x }} \cdot {e^{\dfrac{{ - 1}}{{4 \cdot x}}}}} \right) \cdot dx} = }](/forum/ext/geomar/texintegr/latexrender/pictures/91999040b276f37452d38bf1ae43449c.png)
![\displaystyle{ = \dfrac{{\sqrt \pi }}{2} \cdot \int\limits_0^\infty {\left( {\dfrac{1}{{\sqrt x }} \cdot {e^{\dfrac{{ - 1}}{{4 \cdot x}}}}} \right) \cdot {e^\big{{ - 1 \cdot x}}} \cdot dx} \mathop = \limits^\big{{[2] (s=1)}} \frac{{\sqrt \pi }}{2} \cdot \sqrt {\frac{\pi }{1}} \cdot {e^\big{{ - \sqrt 1 }}} = \frac{\pi }{2\cdot e}} \displaystyle{ = \dfrac{{\sqrt \pi }}{2} \cdot \int\limits_0^\infty {\left( {\dfrac{1}{{\sqrt x }} \cdot {e^{\dfrac{{ - 1}}{{4 \cdot x}}}}} \right) \cdot {e^\big{{ - 1 \cdot x}}} \cdot dx} \mathop = \limits^\big{{[2] (s=1)}} \frac{{\sqrt \pi }}{2} \cdot \sqrt {\frac{\pi }{1}} \cdot {e^\big{{ - \sqrt 1 }}} = \frac{\pi }{2\cdot e}}](/forum/ext/geomar/texintegr/latexrender/pictures/f974372d5176a21a0bbf7c526e3f7f7e.png)
Για την (α) έχω την εντύπωση ότι δεν υπάρχει κλειστή φόρμα (αυτό διερευνάται, καθώς και ο υπολογισμός του β με στοιχειωδέστερα μέσα)
Σεραφείμ Τσιπέλης
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Γενικευμένα Ολοκληρώματα
Μιας και είναι καιρό αναπάντητο, ας δώσω μια λύση.Κοτρώνης Αναστάσιος έγραψε:Ας εξετασθεί ως προς τη σύγκλιση το ολοκλήρωμα
.
Το ολοκλήρωμα συγκλίνει.
Πρώτα ελέγχουμε τη σύγκλιση στο
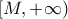 ,
,  .
.Καθώς
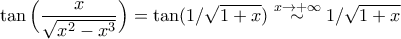 , αρκεί να ελέγξουμε ως προς τη σύγκλιση το
, αρκεί να ελέγξουμε ως προς τη σύγκλιση το 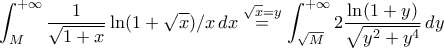 .
.Αλλά
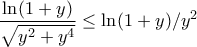 της οποίας το ολοκλήρωμα στο
της οποίας το ολοκλήρωμα στο 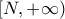 για μεγάλο
για μεγάλο  ελέγχεται εύκολα ότι συγκλίνει.
ελέγχεται εύκολα ότι συγκλίνει.Τώρα κοιτάμε το
![\displaystyle{(0,1]} \displaystyle{(0,1]}](/forum/ext/geomar/texintegr/latexrender/pictures/5ae8012ac41c428517511f1311e3eb17.png) . Καθώς
. Καθώς 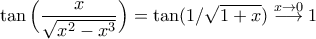 αρκεί να ελέγξουμε το
αρκεί να ελέγξουμε το 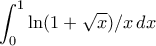 .
.Όμως
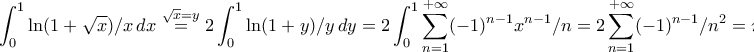
Εσύ....; Θα γίνεις κανίβαλος....;
- Κοτρώνης Αναστάσιος
- Επιμελητής
- Δημοσιεύσεις: 3203
- Εγγραφή: Κυρ Φεβ 22, 2009 11:11 pm
- Τοποθεσία: Μπροστά στο πισί...
- Επικοινωνία:
Re: Γενικευμένα Ολοκληρώματα
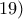 Ας εξετασθεί ως προς τη σύγκλιση το
Ας εξετασθεί ως προς τη σύγκλιση το 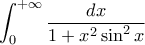 .
.
τελευταία επεξεργασία από Κοτρώνης Αναστάσιος σε Κυρ Νοέμ 07, 2010 9:12 pm, έχει επεξεργασθεί 2 φορές συνολικά.
Εσύ....; Θα γίνεις κανίβαλος....;
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες