
όταν

Αναπάντητο για την ώρα στο μαθλινκσ
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος



 έχουμε μη οριζόμενο λογάριθμο. Ενδιαφέρον έχει η ερώτηση για
έχουμε μη οριζόμενο λογάριθμο. Ενδιαφέρον έχει η ερώτηση για  .
.
Δεν υπάρχει κανένα πρόβλημα.Το ολοκλήρωμα υπάρχει η σαν γενικευμένο Riemann η σαν Lebesgue.Tolaso J Kos έγραψε: ↑Πέμ Νοέμ 03, 2022 8:03 pmΠολλά στραβά βλέπω. π.χ γιαέχουμε μη οριζόμενο λογάριθμο. Ενδιαφέρον έχει η ερώτηση για
.


 και στο τελευταίο ολοκλήρωμα έχουμε P.V
και στο τελευταίο ολοκλήρωμα έχουμε P.V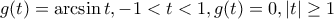

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης