 οι οποίες είναι συνεχείς και τέτοιες ώστε
οι οποίες είναι συνεχείς και τέτοιες ώστε .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Μη αναγνωσμένη δημοσίευση από socrates » Τρί Σεπ 01, 2009 12:29 am
 οι οποίες είναι συνεχείς και τέτοιες ώστε
οι οποίες είναι συνεχείς και τέτοιες ώστε .
.Μη αναγνωσμένη δημοσίευση από Ilias_Zad » Τρί Σεπ 01, 2009 10:20 am
 , για καθε
, για καθε 
 , παιρνουμε
, παιρνουμε  για καθε
για καθε 
 τοτε
τοτε  για καθε
για καθε 
 ποτε
ποτε  τοτε,
τοτε, και
και  για καθε
για καθε 
 , και
, και 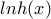 συνεχης στο R προυποθεσεις που με βαση τις συναρτησιακες Cauchy δινουν οτι
συνεχης στο R προυποθεσεις που με βαση τις συναρτησιακες Cauchy δινουν οτι 
 , (
, ( τυχαιος real) για καθε x ή
τυχαιος real) για καθε x ή  για καθε x
για καθε xΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 18 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off