![\displaystyle{{x_\nu } = \sigma \upsilon \nu \left[ {\left( {2\nu - 1} \right)\alpha } \right],\nu = 1,2,...} \displaystyle{{x_\nu } = \sigma \upsilon \nu \left[ {\left( {2\nu - 1} \right)\alpha } \right],\nu = 1,2,...}](/forum/ext/geomar/texintegr/latexrender/pictures/715866971e1b9a6f91f08ac459079c67.png) όπου
όπου 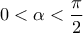 ,
, αποκλίνει ( δεν συγκλίνει σε πραγματικό αριθμό, ούτε στο
 , ούτε στο
, ούτε στο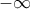 ).
).( Από το βιβλίο Α. Κ. Κυριακόπουλου: «ΑΝΑΛΥΣΗ», τόμους 1, ακολουθίες-Σειρές ,έκδοση 1976, σελίδα 240, άσκηση 757- έχει εξαντληθεί).
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![\displaystyle{{x_\nu } = \sigma \upsilon \nu \left[ {\left( {2\nu - 1} \right)\alpha } \right],\nu = 1,2,...} \displaystyle{{x_\nu } = \sigma \upsilon \nu \left[ {\left( {2\nu - 1} \right)\alpha } \right],\nu = 1,2,...}](/forum/ext/geomar/texintegr/latexrender/pictures/715866971e1b9a6f91f08ac459079c67.png) όπου
όπου 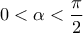 ,
,  , ούτε στο
, ούτε στο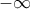 ).
). για κάθε
για κάθε  , η ακολουθία δεν συγκλίνει ούτε στο
, η ακολουθία δεν συγκλίνει ούτε στο  ούτε στο
ούτε στο  .
.  .
. μας δείχνει ότι αν το όριο της
μας δείχνει ότι αν το όριο της  είναι
είναι  , τότε το όριο της
, τότε το όριο της  είναι
είναι  .
. μας δείχνει ότι αν το όριο της
μας δείχνει ότι αν το όριο της  είναι
είναι  , τότε
, τότε 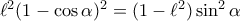 .
. . Άρα θα υπάρχει
. Άρα θα υπάρχει  ώστε
ώστε  θα έχουμε
θα έχουμε  και άρα
και άρα 
 θα έχουμε
θα έχουμε  και άρα
και άρα 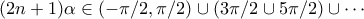
 της μορφής
της μορφής 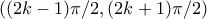 ώστε
ώστε  για κάθε
για κάθε  . Αυτό όμως είναι άτοπο επειδή
. Αυτό όμως είναι άτοπο επειδή  και το
και το  έχει μήκος
έχει μήκος  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες