Έστω
 ένα μη κενό και κλειστό υποσύνολο του
ένα μη κενό και κλειστό υποσύνολο του  (εννοείται με τη συνήθη τοπολογία).
(εννοείται με τη συνήθη τοπολογία).Θεωρούμε την απεικόνιση
 .
.Αποδείξτε ότι το
 είναι κυρτό αν, και μόνο αν, η
είναι κυρτό αν, και μόνο αν, η  είναι κυρτή στο
είναι κυρτή στο  .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 ένα μη κενό και κλειστό υποσύνολο του
ένα μη κενό και κλειστό υποσύνολο του  (εννοείται με τη συνήθη τοπολογία).
(εννοείται με τη συνήθη τοπολογία). .
. είναι κυρτό αν, και μόνο αν, η
είναι κυρτό αν, και μόνο αν, η  είναι κυρτή στο
είναι κυρτή στο  .
.
 μη κυρτό και έστω σημεία
μη κυρτό και έστω σημεία  και
και  στο εσωτερικό του
στο εσωτερικό του  με
με  . Τότε
. Τότε  και
και  λόγω κλειστότητας. Άρα η
λόγω κλειστότητας. Άρα η  είναι μη κυρτή.
είναι μη κυρτή.
 κυρτό,
κυρτό,  και
και  με
με  . Ορίζουμε
. Ορίζουμε  με
με  και
και  (υπάρχουν λόγω κλειστότητας) και θέτουμε
(υπάρχουν λόγω κλειστότητας) και θέτουμε  και
και  . Ισχύει
. Ισχύει  λόγω κυρτότητας.
λόγω κυρτότητας. . Άρα η
. Άρα η  είναι κυρτή.
είναι κυρτή.Πού είσαι βρε Δημήτρη!!dement έγραψε:...
Ακόμη ένας τρόπος (σχεδόν ίδιος)dement έγραψε:
Έστωμη κυρτό και έστω σημεία
και
στο εσωτερικό του
με
. Τότε
και
λόγω κλειστότητας. Άρα η
είναι μη κυρτή.
 είναι κυρτή στο
είναι κυρτή στο  . Θα δείξουμε ότι το
. Θα δείξουμε ότι το  είναι κυρτό.
είναι κυρτό. και
και ![\displaystyle{m\in\left[0,1\right]} \displaystyle{m\in\left[0,1\right]}](/forum/ext/geomar/texintegr/latexrender/pictures/b25b98ab055a080eafe7ea87cce97aec.png) . Τότε,
. Τότε,  και
και είναι κυρτή έχουμε
είναι κυρτή έχουμε
 , όπως θέλαμε.
, όπως θέλαμε.Γεια σου γίγαντα Τάσο. Χαίρομαι που έχεις πάντα το ίδιο άβαταρ.Κοτρώνης Αναστάσιος έγραψε:Πού είσαι βρε Δημήτρη!!dement έγραψε:...
 είναι ένας απειροδιάστατος χώρος
είναι ένας απειροδιάστατος χώρος  και
και 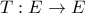
 δεν είναι συμπαγής.
δεν είναι συμπαγής.![\displaystyle{P(z)=a_0+a_1\,z+...a_n\,z^n\in\mathbb{C}[z]\,\,,a_{n}\neq 0} \displaystyle{P(z)=a_0+a_1\,z+...a_n\,z^n\in\mathbb{C}[z]\,\,,a_{n}\neq 0}](/forum/ext/geomar/texintegr/latexrender/pictures/f44c39435c08b548261d2c45ad744882.png) με σύνολο ριζών το
με σύνολο ριζών το  ,
,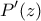 ανήκει στην κυρτή θήκη του
ανήκει στην κυρτή θήκη του  .
.
Με χρήση τωνBAGGP93 έγραψε:ΑΣΚΗΣΗ 107
Ανείναι ένας απειροδιάστατος χώρος
και
είναι μια γραμμική, 1-1 και επί απεικόνιση, δείξτε ότι ηδεν είναι συμπαγής.
 είναι αντιστρέψιμος τελεστής (δηλαδή φραγμένος) τότε και ο
είναι αντιστρέψιμος τελεστής (δηλαδή φραγμένος) τότε και ο  είναι φραγμένος.
είναι φραγμένος. ήταν συμπαγής και αντιστρέψιμος, τότε θα ήταν συμπαγής και ο
ήταν συμπαγής και αντιστρέψιμος, τότε θα ήταν συμπαγής και ο  . Αλλά τότε η μοναδιαία σφαίρα θα ήταν συμπαγές σύνολο, άτοπο στους απειροδιάστατους (Riesz).
. Αλλά τότε η μοναδιαία σφαίρα θα ήταν συμπαγές σύνολο, άτοπο στους απειροδιάστατους (Riesz).Πρόκειται για το Θεώρημα Gauss-Lucas.BAGGP93 έγραψε: ΑΣΚΗΣΗ 108
Ανμε σύνολο ριζών το
,
τότε αποδείξτε ότι κάθε ρίζα της παραγώγουανήκει στην κυρτή θήκη του
.
 είναι οι εστίες της έλλειψης που εφάπτεται στο τρίγωνο που ορίζουν οι ρίζες του
είναι οι εστίες της έλλειψης που εφάπτεται στο τρίγωνο που ορίζουν οι ρίζες του  . Είμαι σίγουρος ότι το Google θα δώσει άριστες παραπομπές (δεν το ψάχνω).
. Είμαι σίγουρος ότι το Google θα δώσει άριστες παραπομπές (δεν το ψάχνω).  . Αξιοσημείωτη συμβολή σε αυτή την κατεύθυνση είναι από τον Μανώλη Κατσοπρινάκη, συνταξιούχο σήμερα Καθηγητή στο Μαθηματικό Κρήτης.
. Αξιοσημείωτη συμβολή σε αυτή την κατεύθυνση είναι από τον Μανώλη Κατσοπρινάκη, συνταξιούχο σήμερα Καθηγητή στο Μαθηματικό Κρήτης.  με τις εξής ιδιότητες :
με τις εξής ιδιότητες :
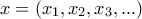 και
και  τότε
τότε 
 συμβολίζουμε τον υποχώρο όλων των συγκλινουσών ακολουθιών, τότε
συμβολίζουμε τον υποχώρο όλων των συγκλινουσών ακολουθιών, τότε  για κάθε
για κάθε 
Νίκο, πρόκειται για τα λεγόμενα Banach Limits (βλέπε π.χ. εδώ) τα οποία είναι αρκετά στάνταρ θεωρία στα βιβλία Συναρτησιακής Ανάλυσης. Η απόδειξη γίνεται με χρήση του Θεωρήματος Hahn-Banach.nickthegreek έγραψε:Προτείνω την ακόλουθη ενδιαφέρουσα άσκηση :
Nα αποδείξετε ότι υπάρχειμε τις εξής ιδιότητες :
1)
2) Ανκαι
τότε
3) Aν μεσυμβολίζουμε τον υποχώρο όλων των συγκλινουσών ακολουθιών, τότε
για κάθε
Φιλικά,
Νίκος
 τέτοια συναρτησοειδή.
τέτοια συναρτησοειδή.Ευχαριστώ κύριε Μιχάλη! Δεν γνώριζα ότι υπάρχει ειδική ορολογία για το συγκεκριμένο συναρτησοειδές. Δίνω και τη λύση μου για να κλείσει η άσκηση :Mihalis_Lambrou έγραψε:Νίκο, πρόκειται για τα λεγόμενα Banach Limits (βλέπε π.χ. εδώ) τα οποία είναι αρκετά στάνταρ θεωρία στα βιβλία Συναρτησιακής Ανάλυσης. Η απόδειξη γίνεται με χρήση του Θεωρήματος Hahn-Banach.nickthegreek έγραψε:Προτείνω την ακόλουθη ενδιαφέρουσα άσκηση :
Nα αποδείξετε ότι υπάρχειμε τις εξής ιδιότητες :
1)
2) Ανκαι
τότε
3) Aν μεσυμβολίζουμε τον υποχώρο όλων των συγκλινουσών ακολουθιών, τότε
για κάθε
Φιλικά,
Νίκος
Μπορούμε ακόμη να βρούμε τέτοιο συναρτησοειδές που ικανοποεί επιπλέον κάποια συνθήκη "θετικότητας" (βλέπε την συνθήκη 2 στην παραπάνω παραπομπή). Τέλος, αν θυμάμαι καλά (αλλά ομολογώ ότι είμαι κουρασμένος μετά από ολοήμερο ταξίδι στο εξωτερικό, και δεν το ψάχνω) υπάρχουντέτοια συναρτησοειδή.
 χώρος με νόρμα και
χώρος με νόρμα και  υποχώρος. Έστω
υποχώρος. Έστω  τέτοιο ώστε
τέτοιο ώστε  . Τότε υπάρχει
. Τότε υπάρχει  τέτοιο ώστε
τέτοιο ώστε  ,
,  και
και 
 και ορίζω ένα συναρτησοειδές
και ορίζω ένα συναρτησοειδές  στο
στο  ως εξής :
ως εξής :  . Αν
. Αν  έχουμε
έχουμε  οπότε
οπότε  . Όμως για
. Όμως για  έχω
έχω  . Παίρνω το infimum ως προς
. Παίρνω το infimum ως προς  και συμπεραίνω ότι
και συμπεραίνω ότι  . Άρα
. Άρα  . To ζητούμενο τώρα προκύπτει από μια μορφή του Hahn - Banach .
. To ζητούμενο τώρα προκύπτει από μια μορφή του Hahn - Banach . 
 και
και  . Τότε
. Τότε  (γιατί;) . Άρα υπάρχει σύμφωνα με το λήμμα συναρτησοειδές
(γιατί;) . Άρα υπάρχει σύμφωνα με το λήμμα συναρτησοειδές  που ικανοποιεί τις συνθήκες
που ικανοποιεί τις συνθήκες  του προβλήματος. Για την
του προβλήματος. Για την  χρειάζεται λίγη περισσότερη δουλειά. Παρατηρήστε ότι ισοδύναμα αρκεί να δείξουμε ότι
χρειάζεται λίγη περισσότερη δουλειά. Παρατηρήστε ότι ισοδύναμα αρκεί να δείξουμε ότι  όπου με
όπου με  συμβολίζουμε τον υποχώρο των ακολουθιών που συγκλίνουν στο μηδέν. Γρήγορα σκεφτόμαστε ότι το πρόβλημα θα λυνόταν αν
συμβολίζουμε τον υποχώρο των ακολουθιών που συγκλίνουν στο μηδέν. Γρήγορα σκεφτόμαστε ότι το πρόβλημα θα λυνόταν αν  . Κάτι τέτοιο όμως δεν ισχύει! Δοκιμάζουμε λοιπόν τον υποχώρο
. Κάτι τέτοιο όμως δεν ισχύει! Δοκιμάζουμε λοιπόν τον υποχώρο  των ακολουθιών αυτών που έχουν πεπερασμένες μη μηδενικές "συντεταγμένες". Εύκολα προκύπτει ότι
των ακολουθιών αυτών που έχουν πεπερασμένες μη μηδενικές "συντεταγμένες". Εύκολα προκύπτει ότι  και έχουμε ότι
και έχουμε ότι  . Το ζητούμενο έπεται.
. Το ζητούμενο έπεται. , όπου
, όπου 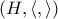
 , είναι ανοικτό υποσύνολο της άλγεβρας
, είναι ανοικτό υποσύνολο της άλγεβρας  ,
,  .
.BAGGP93 έγραψε:ΑΣΚΗΣΗ 110
Να αποδείξετε ότι το σύνολο, όπου
είναι χώρος, είναι ανοικτό υποσύνολο της άλγεβρας
,
.
 με μονάδα και συμβολίζουμε με
με μονάδα και συμβολίζουμε με  το σύνολο των αντιστρέψιμων στοιχείων τότε το
το σύνολο των αντιστρέψιμων στοιχείων τότε το  είναι ανοικτό. Για την απόδειξη, μπορεί κάποιος να αποδείξει ότι αν
είναι ανοικτό. Για την απόδειξη, μπορεί κάποιος να αποδείξει ότι αν  τότε το
τότε το  είναι αντιστρέψιμο και
είναι αντιστρέψιμο και  . H απόδειξη αυτού γίνεται με χρήση της σειράς
. H απόδειξη αυτού γίνεται με χρήση της σειράς  και έχει ξαναγίνει νομίζω σε αυτό το topic, οπότε δεν τη δίνω.
και έχει ξαναγίνει νομίζω σε αυτό το topic, οπότε δεν τη δίνω.  τότε το
τότε το  είναι αντιστρέψιμο! Γιατί έχουμε
είναι αντιστρέψιμο! Γιατί έχουμε  και από το παραπάνω το
και από το παραπάνω το 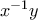 είναι αντιστρέψιμο και άρα το ίδιο ισχύει και για το
είναι αντιστρέψιμο και άρα το ίδιο ισχύει και για το  .
.  μια Banach άλγεβρα με μονάδα.
μια Banach άλγεβρα με μονάδα. είναι συνεχής
είναι συνεχής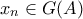 και
και  τότε
τότε 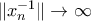
 τότε το
τότε το  έχει τοπολογικούς μηδενοδιαιρέτες , δηλαδή απλά υπάρχει ακολουθία
έχει τοπολογικούς μηδενοδιαιρέτες , δηλαδή απλά υπάρχει ακολουθία στη μοναδιαία σφαίρα του
στη μοναδιαία σφαίρα του  τέτοια ώστε
τέτοια ώστε  και
και  .
. . Αποδείξτε ότι αν
. Αποδείξτε ότι αν  είναι ένα μετρήσιμο υποσύνολο του
είναι ένα μετρήσιμο υποσύνολο του 
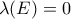 , τότε
, τότε  .
. συμβολίζουμε το μέτρο
συμβολίζουμε το μέτρο  στο
στο  .
.Γεια σου Νίκο.nickthegreek έγραψε:
Ας προτείνω μερικές ακόμη γνωστές ιδιότητες για επίλυση :
ΑΣΚΗΣΗ 111
Έστωμια Banach άλγεβρα με μονάδα.
1) H πράξηείναι συνεχής
2) Ανκαι
τότε
3) Αντότε το
έχει τοπολογικούς μηδενοδιαιρέτες , δηλαδή απλά υπάρχει ακολουθία
στη μοναδιαία σφαίρα του
τέτοια ώστε
και
.
 .
. ώστε
ώστε  .
. , αντίστοιχα.
, αντίστοιχα. έχουμε
έχουμε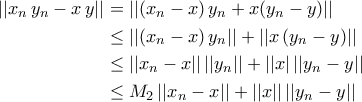
 και
και  με
με  , τότε
, τότε και
και 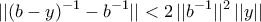 .
. είναι τοπολογική ομάδα.
είναι τοπολογική ομάδα. (διότι αλλιώς,
(διότι αλλιώς, 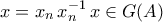 ), έπεται ότι
), έπεται ότι .
. διότι
διότι  ενώ
ενώ  .
. .
. , (
, ( - ανοιχτό), έπεται ότι
- ανοιχτό), έπεται ότι 
 στοιχείων του
στοιχείων του  τέτοια, ώστε
τέτοια, ώστε  .
. και άρα,
και άρα, .
. με
με 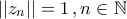 και
και . Επίσης,
. Επίσης,  .
. έχει τοπολογικούς διαιρέτες.
έχει τοπολογικούς διαιρέτες.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες