 .
.Ας δούμε μετά και αυτό :
 .
.Δεν το χω λύσει...
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 .
. .
.


![\displaystyle{\begin{array}{l}
= - \frac{\pi }{{2\sqrt {{e^2} - 1} }}\int\limits_e^{ + \infty } {\frac{{y - \sqrt {{e^2} - 1} - y - \sqrt {{e^2} - 1} }}{{\left( {y - \sqrt {{e^2} - 1} } \right)\left( {y + \sqrt {{e^2} - 1} } \right)}}dy} = \\
= - \frac{\pi }{{2\sqrt {{e^2} - 1} }}\int\limits_e^{ + \infty } {\left( {\frac{1}{{y + \sqrt {{e^2} - 1} }} - \frac{1}{{y - \sqrt {{e^2} - 1} }}} \right)} dy = \\
= - \frac{\pi }{{2\sqrt {{e^2} - 1} }}\left[ {\ln \left| {\frac{{y + \sqrt {{e^2} - 1} }}{{y - \sqrt {{e^2} - 1} }}} \right|} \right]_e^{ + \infty } = \\
\end{array}} \displaystyle{\begin{array}{l}
= - \frac{\pi }{{2\sqrt {{e^2} - 1} }}\int\limits_e^{ + \infty } {\frac{{y - \sqrt {{e^2} - 1} - y - \sqrt {{e^2} - 1} }}{{\left( {y - \sqrt {{e^2} - 1} } \right)\left( {y + \sqrt {{e^2} - 1} } \right)}}dy} = \\
= - \frac{\pi }{{2\sqrt {{e^2} - 1} }}\int\limits_e^{ + \infty } {\left( {\frac{1}{{y + \sqrt {{e^2} - 1} }} - \frac{1}{{y - \sqrt {{e^2} - 1} }}} \right)} dy = \\
= - \frac{\pi }{{2\sqrt {{e^2} - 1} }}\left[ {\ln \left| {\frac{{y + \sqrt {{e^2} - 1} }}{{y - \sqrt {{e^2} - 1} }}} \right|} \right]_e^{ + \infty } = \\
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/13e55222609edcbe4320f63e69af3a6d.png)
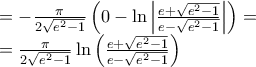
Ωραίος. Και εγώ κάτι τέτοιο έχω βγάλει με παρόμοιο τρόπο.Το βιβλίο δίνειmathxl έγραψε:Το ορισμένο μου βγήκε λίγο μεγάλο
 , που προφανώς είνια λάθος, τουλάχιστον λόγω του ριζικού. Τωρα το τόξο συνημιτόνου δεν ξέρω από πού βγαίνει...
, που προφανώς είνια λάθος, τουλάχιστον λόγω του ριζικού. Τωρα το τόξο συνημιτόνου δεν ξέρω από πού βγαίνει... Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες