Θέλω να βρω τα
 ,
,  και τα σημεία συσσώρευσης των παρακάτω ακολουθιών:
και τα σημεία συσσώρευσης των παρακάτω ακολουθιών: 1.

2.
![a_n=\sqrt[n]{n+(-1)^nn} a_n=\sqrt[n]{n+(-1)^nn}](/forum/ext/geomar/texintegr/latexrender/pictures/2b77e5993b5b461674a5a19c650a7be9.png)
3.

4.
![a_n=(-1)^{\frac{n(n+1)}{2}}\sqrt[n]{1+\frac{1}{n}} a_n=(-1)^{\frac{n(n+1)}{2}}\sqrt[n]{1+\frac{1}{n}}](/forum/ext/geomar/texintegr/latexrender/pictures/5e29ad74f8cff38c0c004f5b87477719.png)
Έχω κάνει τα εξής:
1.


Οπότε η
 έχει τα σημεία συσσώρευσης τα
έχει τα σημεία συσσώρευσης τα  και
και  .
. Άρα
 και
και  .
. 2.
![a_{2k}=\sqrt[2k]{2k+(-1)^{2k}2k}=\sqrt[2k]{4k}=2^{\frac{1}{k}}\left ( k^{\frac{1}{k}}\right )^{\frac{1}{2}}\Rightarrow \lim_{k\rightarrow \infty}a_{2k}=1 a_{2k}=\sqrt[2k]{2k+(-1)^{2k}2k}=\sqrt[2k]{4k}=2^{\frac{1}{k}}\left ( k^{\frac{1}{k}}\right )^{\frac{1}{2}}\Rightarrow \lim_{k\rightarrow \infty}a_{2k}=1](/forum/ext/geomar/texintegr/latexrender/pictures/bd4b09f3f91998fa102867509d0f10ff.png)
![a_{2k-1}=\sqrt[2k-1]{2k-1+(-1)^{2k-1}(2k-1)}=0\Rightarrow \lim_{k\rightarrow \infty}a_{2k-1}=0 a_{2k-1}=\sqrt[2k-1]{2k-1+(-1)^{2k-1}(2k-1)}=0\Rightarrow \lim_{k\rightarrow \infty}a_{2k-1}=0](/forum/ext/geomar/texintegr/latexrender/pictures/b41b1a9ab4bff88470017838ec232bb1.png)
Οπότε η
 έχει τα σημεία συσσώρευσης τα
έχει τα σημεία συσσώρευσης τα  και
και  .
. Άρα
 και
και  .
. 3.


Οπότε η
 έχει τα σημεία συσσώρευσης τα
έχει τα σημεία συσσώρευσης τα  και
και  .
. Άρα
 και
και  .
. Είναι σωστά αυτά που έχω κάνει μέχρι εδώ;
4.
![a_n=(-1)^{\frac{n(n+1)}{2}}\sqrt[n]{1+\frac{1}{n}} a_n=(-1)^{\frac{n(n+1)}{2}}\sqrt[n]{1+\frac{1}{n}}](/forum/ext/geomar/texintegr/latexrender/pictures/5e29ad74f8cff38c0c004f5b87477719.png)
Υπολόγισα ττις υπακολουθίες
 και
και  αλλά δεν μπόρεσα να βρω το όριο τους. Υπολογίζουμε με άλλο τρόπο σε αυτή την περίπτωση τα σημεία συσσώρευσης;
αλλά δεν μπόρεσα να βρω το όριο τους. Υπολογίζουμε με άλλο τρόπο σε αυτή την περίπτωση τα σημεία συσσώρευσης;
![\sqrt [n] n \sqrt [n] n](/forum/ext/geomar/texintegr/latexrender/pictures/8a9ec4f98db8800712041e1d7a5ebcab.png) που έχει "πολύ μεγαλύτερη υπόρριζη ποσότητα" από την
που έχει "πολύ μεγαλύτερη υπόρριζη ποσότητα" από την ![\sqrt[n]{1+\frac{1}{n}} \sqrt[n]{1+\frac{1}{n}}](/forum/ext/geomar/texintegr/latexrender/pictures/96acdfc009ff3f61b428cf8f361b279e.png) . Τολμώ να συστήσω να βλέπεις την ουσία των πραγμάτων και όχι σκέτα τους τύπους χωρίς την κατανόησή τους.
. Τολμώ να συστήσω να βλέπεις την ουσία των πραγμάτων και όχι σκέτα τους τύπους χωρίς την κατανόησή τους.![1 \le \sqrt[n]{1+\frac{1}{n}} \le \sqrt[n]{2} 1 \le \sqrt[n]{1+\frac{1}{n}} \le \sqrt[n]{2}](/forum/ext/geomar/texintegr/latexrender/pictures/96cc0d3db5dc8285ee1862ac1ae37fbf.png)

 είναι είτε άρτιο είτε περιττό. Αφού έχουμε βρεί τα όρια για τις υπακολουθίες
είναι είτε άρτιο είτε περιττό. Αφού έχουμε βρεί τα όρια για τις υπακολουθίες  είναι σαφές ότι πρέπει να εξετάσεις τις εκδοχές
είναι σαφές ότι πρέπει να εξετάσεις τις εκδοχές  διότι σε αυτά αλλάζει η τιμή του όρου
διότι σε αυτά αλλάζει η τιμή του όρου  . Συγκεκριμένα, η
. Συγκεκριμένα, η  καθώς πάει
καθώς πάει  και λοιπά.
και λοιπά. η περιοδικότητα είναι ανά τέσσερις όρους αφού πάει
η περιοδικότητα είναι ανά τέσσερις όρους αφού πάει  .
. είναι περιοδική με περίοδο 4, αφού
είναι περιοδική με περίοδο 4, αφού  . Άρα
. Άρα  και
και  .
. ![c_n=\sqrt[n]{1+\frac{1}{n}}\rightarrow 1 c_n=\sqrt[n]{1+\frac{1}{n}}\rightarrow 1](/forum/ext/geomar/texintegr/latexrender/pictures/ea6d6ac6de08644b66c86b3826a861c5.png) . Άρα
. Άρα  .
.  υπάρχουν, ισχύει
υπάρχουν, ισχύει  και
και  , σωστά;
, σωστά;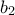 , το παραπάνω ΔΕΝ ΕΙΝΑΙ ΜΑΘΗΜΑΤΙΚΗ ΑΠΟΔΕΙΞΗ. Είναι απλά έλεγχος μικρών δεικτών. Σε διαγώνισμα θα είχες πρόβλημα!
, το παραπάνω ΔΕΝ ΕΙΝΑΙ ΜΑΘΗΜΑΤΙΚΗ ΑΠΟΔΕΙΞΗ. Είναι απλά έλεγχος μικρών δεικτών. Σε διαγώνισμα θα είχες πρόβλημα! ΔΕΝ υπάρχει. Άλλο εννοείς, Αν πάλι εργαστείς μόνο με limsup, ο παραπάνω τύπος δεν ισχύει. Πάρε για παράδειγμα
ΔΕΝ υπάρχει. Άλλο εννοείς, Αν πάλι εργαστείς μόνο με limsup, ο παραπάνω τύπος δεν ισχύει. Πάρε για παράδειγμα  εναλλάξ και
εναλλάξ και  ίσον
ίσον  , οπότε
, οπότε  . Δες το!
. Δες το!