Γενικευμένο λογαριθμικό ολοκλήρωμα

#1

Για $0<\alpha<\beta$ , να υπολογισθεί το $\displaystyle\int_{0}^{+\infty}\frac{\log{x}}{(x+\alpha)(x+\beta)}\,dx\,.$

Tolaso J Kos · #2

grigkost έγραψε:Για $0<\alpha<\beta$ , να υπολογισθεί το $\displaystyle\int_{0}^{+\infty}\frac{\log{x}}{(x+\alpha)(x+\beta)}\,dx\,.$

$\displaystyle{\int_{0}^{\infty} \frac{\log x}{\left ( x+\alpha \right )\left ( x+\beta \right )} \, {\rm d}x = \frac{1}{2 (\beta - \alpha) } \left [ \log^2 \beta - \log^2 \alpha \right ]}$ Άκυρα τα παραπάνω. Ισχύουν μόνο αν οι πόλοι είναι μέσα. Το αποτέλεσμα είναι σωστό αλλά πρέπει να φτιάξω τη λύση. Το βράδυ τώρα.

Συγνώμη. Θα επανέλθω.

#3

Μια λύση:

Για τον υπολογισμό του $\displaystyle\int_{0}^{+\infty}\frac{\log{x}}{(x+\alpha)(x+\beta)}\,dx\,,\quad 0<\alpha<\beta$ , θεωρούμε την συνάρτηση $f(z)=\dfrac{{\rm{Log}}^2{z}}{(z-\alpha)(z-\beta)}\,,\quad z\in\mathbb{C}\setminus\{x+0i\;|\;x\leqslant0\}$ , η οποία είναι μερόμορφη στο ${\mathbb{C}}\setminus\{x+0i\;|\;x\leqslant0\}$ με απλούς πόλους τους $z=\alpha$ , $z=\beta$ . Θεωρούμε, επίσης, την απλή, κλειστή καμπύλη $\gamma$ , η οποία είναι το άθροισμα του θετικά προσανατολισμένου τόξου $C_r:=\big\{r\,{\rm{e}}^{it}\in{\mathbb{C}}\;\big|\; t\in(-\pi+\varepsilon,\pi-\varepsilon]\big\}\,, \; r\to+\infty\,,\;\varepsilon\to0^+\,,$ του ευθυγράμμου τμήματος $\ell:=\big\{(r+\delta-t)\,{\rm{e}}^{i\pi}\in{\mathbb{C}}\;\big|\; t\in(\delta,r)\big\}$ , του αρνητικά προσανατολισμένου τόξου $C_\delta:=\big\{\delta\,{\rm{e}}^{-it}\in{\mathbb{C}}\;\big|\; t\in(-\pi+\varepsilon,\pi-\varepsilon]\big\}\,, \;\delta\to0^{+}\,,\;\varepsilon\to0^+\,,$ και του ευθυγράμμου τμήματος $-\ell:=\big\{t\,{\rm{e}}^{-i\pi}\in{\mathbb{C}}\;\big|\; t\in(\delta,r)\big\}$ .
[attachment=0]contour.png[/attachment] Επομένως $\begin{aligned} {\rm{Res}\,}\big(f(z), z=\alpha\big)&=\frac{1}{0!}\,\mathop{\lim}\limits_{z\to\alpha}\bigg(( z-\alpha)\,\dfrac{{\rm{Log}\,}^2{z}}{(z-\alpha)(z-\beta)}\bigg)\\\noalign{\vspace{0.2cm}} &=\mathop{\lim}\limits_{z\to\alpha}\dfrac{{\rm{Log}\,}^2{z}}{z-\beta}\\\noalign{\vspace{0.2cm}} &= \dfrac{\log^2{\alpha}}{\alpha-\beta}\,,\\\noalign{\vspace{0.2cm}} {\rm{Res}\,}\big(f(z), z=\beta\big)&=\frac{1}{0!}\,\mathop{\lim}\limits_{z\to\beta}\bigg(( z-\beta)\,\dfrac{{\rm{Log}\,}^2{z}}{(z-\alpha)(z-\beta)}\bigg)\\\noalign{\vspace{0.2cm}} &=\mathop{\lim}\limits_{z\to\beta}\dfrac{{\rm{Log}\,}^2{z}}{z-\alpha}\\\noalign{\vspace{0.2cm}} &=\dfrac{\log^2{\beta}}{\beta-\alpha} \end{aligned}$ και $\begin{aligned} \displaystyle\oint_{\gamma}{f(z)\,dz}&=2\pi i\;\cancelto{1}{{\rm{I}\,}\big(\gamma, z=\alpha\big)}\,{\rm{Res}\,}\big(f(z), z=\alpha\big)+2\pi i\;\cancelto{1}{{\rm{I}\,}\big(\gamma, z=\beta\big)}\,{\rm{Res}\,}\big(f(z), z=\beta\big)\\\noalign{\vspace{0.2cm}} &=2\pi i\,\dfrac{\log^2{\alpha}}{\alpha-\beta}+2\pi i\,\dfrac{\log^2{\beta}}{\beta-\alpha}\\\noalign{\vspace{0.2cm}} &=2\pi i\,\dfrac{\log^2\beta-\log^2\alpha}{\beta-\alpha}&\Longrightarrow\\\noalign{\vspace{0.2cm}} \oint_{C_{r}}{f(z)\,dz}&+\oint_{\ell}{f(z)\,dz}+\oint_{C_{\delta}}{f(z)\,dz}+\oint_{-\ell}{f(z)\,dz}=2\pi i\,\dfrac{\log^2\beta-\log^2\alpha}{\beta-\alpha}\qquad(1)\,. \end{aligned}$ Επίσης $\begin{aligned} \displaystyle\oint_{\ell}{f(z)\,dz}&=\int_{\delta}^{r}{\dfrac{{\rm{Log}\,}^2\big((r+\delta-t)\,{\rm{e}}^{i\pi}\big)\,\big((r+\delta-t)\,{\rm{e}}^{i\pi}\big)'}{\big((r+\delta-t)\,{\rm{e}}^{i\pi}-\alpha\big)\big((r+\delta-t)\,{\rm{e}}^{i\pi}-\beta\big)}\,dt}\\\noalign{\vspace{0.2cm}} &=\int_{\delta}^{r}{\dfrac{\big(\log|-r-\delta+t|+i\,\pi\big)^2}{(-r-\delta+t-\alpha)(-r-\delta+t-\beta)}\,dt}\\\noalign{\vspace{0.2cm}} &\mathop{=\!=\!=\!=\!=\!=\!=}\limits^{\begin{subarray}{c} {s\,=\,r+\delta-t}\\\noalign{\vspace{0.05cm}} {ds\,=\,-dt}\\\noalign{\vspace{0.05cm}} \end{subarray}}\,\int_{\delta}^{r}{\dfrac{\big(\log{s}+i\,\pi\big)^2}{(-s-\alpha)(-s-\beta)}\,ds}\\\noalign{\vspace{0.2cm}} &=\int_{\delta}^{r}{\dfrac{\big(\log{t}+i\,\pi\big)^2}{(t+\alpha)(t+\beta)}\,dt}\,,\\\noalign{\vspace{0.2cm}} \displaystyle\oint_{-\ell}{f(z)\,dz}&=\int_{\delta}^{r}{\dfrac{{\rm{Log}\,}^2\big(t\,{\rm{e}}^{-i\pi}\big)\,\big(t\,{\rm{e}}^{-i\pi}\big)'}{\big(t\,{\rm{e}}^{-i\pi}-\alpha\big)\big(t\,{\rm{e}}^{-i\pi}-\beta\big)}\,dt}\\\noalign{\vspace{0.2cm}} &=-\int_{\delta}^{r}{\dfrac{\big(\log|{-t}|-i\,\pi\big)^2}{(-t-\alpha)(-t-\beta)}\,dt}\\\noalign{\vspace{0.2cm}} &=-\int_{\delta}^{r}{\dfrac{\big(\log{t}-i\,\pi\big)^2}{(t+\alpha)(t+\beta)}\,dt}\hspace{3.0cm}\Rightarrow\\\noalign{\vspace{0.2cm}} \int_{\ell}{f(z)\,dz}+\int_{-\ell}{f(z)\,dz}&=\int_{\delta}^{r}{\dfrac{\big(\log{t}+i\,\pi\big)^2}{(t+\alpha)(t+\beta)}\,dt}-\int_{\delta}^{r}{\dfrac{\big(\log{t}-i\,\pi\big)^2}{(t+\alpha)(t+\beta)}\,dt}\\\noalign{\vspace{0.2cm}} &=\int_{\delta}^{r}{\dfrac{4\pi\,i\,\log{t}}{(t+\alpha)(t+\beta)}\,dt}\,. \end{aligned}$ Με την βοήθεια του θεωρήματος εκτίμησης αποδεικνύεται ότι $\displaystyle\mathop{\lim}\limits_{r\to+\infty}\oint_{C_{r}}{f(z)\,dz}=\mathop{\lim}\limits_{\delta\to0^{+}}\oint_{C_{\delta}}{f(z)\,dz}=0\,.$ Επομένως από την (1)

και τα παραπάνω προκύπτει $\begin{aligned} \mathop{\lim}\limits_{\begin{subarray}{c} {r\to+\infty}\\\noalign{\vspace{0.05cm}} {\delta\to0^+} \end{subarray}}\int_{\delta}^{r}{\dfrac{4\pi\,i\,\log{t}}{(t+\alpha)(t+\beta)}\,dt}+\cancelto{0}{\mathop{\lim}\limits_{\begin{subarray}{c} {r\to+\infty}\\\noalign{\vspace{0.05cm}} {\delta\to0^+} \end{subarray}}\int_{C_{r}}{f(z)\,dz}}+\cancelto{0}{\mathop{\lim}\limits_{\begin{subarray}{c} {r\to+\infty}\\\noalign{\vspace{0.05cm}} {\delta\to0^+} \end{subarray}}\int_{C_{\delta}}{f(z)\,dz}}&=2\pi i\,\dfrac{\log^2\beta-\log^2\alpha}{\beta-\alpha} &\Rightarrow\\\noalign{\vspace{0.2cm}} \mathop{\lim}\limits_{\begin{subarray}{c} {r\to+\infty}\\\noalign{\vspace{0.05cm}} {\delta\to0^+} \end{subarray}}\int_{\delta}^{r}{\dfrac{\log{t}}{(t+\alpha)(t+\beta)}\,dt}&=\dfrac{\log^2\beta-\log^2\alpha}{2\,(\beta-\alpha)} &\Rightarrow\\\noalign{\vspace{0.2cm}} \int_{0}^{+\infty}{\dfrac{\log{t}}{(t+\alpha)(t+\beta)}\,dt}&=\dfrac{\log^2\beta-\log^2\alpha}{2\,(\beta-\alpha)}\,. \end{aligned}$

Tolaso J Kos · #4

grigkost έγραψε:Για τον υπολογισμό του $\displaystyle\int_{0}^{+\infty}\frac{\log{x}}{(x+\alpha)(x+\beta)}\,dx\,,\quad 0<\alpha<\beta$ , θεωρούμε την συνάρτηση $f(z)=\dfrac{{\rm{Log}}^2{z}}{(z-\alpha)(z-\beta)}\,,\quad z\in\mathbb{C}\setminus\{x+0i\;|\;x\leqslant0\}$

Είχα στο νού μου αυτή τη συνάρτηση και κατά λάθος στο προηγούμενο μήνυμα έγραψα άλλη συνάρτηση και αναγκάστηκα να το σβήσω. Έτσι λοιπόν ο τύπος που είχα δώσει τότε λέει:
$\displaystyle{\int_0^{\infty} \frac{\log x}{(x+\alpha) (x + \beta)}\; {\rm d}x = -\frac{1}{2} \sum_{k} {\rm Res}_{z = z_k} \frac{\log^2 z}{(z-\alpha)(z - \beta)} + i \pi \sum_{k} {\rm Res}_{z =z_k} \frac{\log z}{(z-\alpha)(z- \beta)}}$ όπου δίδει το σωστό αποτέλεσμα.

Γενικότερα ο παραπάνω τύπος που προκύπτει από εφαρμογή του keyhole contour σκοτώνει εύκολα ολοκληρώματα της μορφής "λογάριθμος επί πολυώνυμο". Πάντως θα ήθελα να δω κάτι με πραγματική ανάλυση.

Πάντως δε φαίνεται να είναι γνωστό σαν αποτέλεσμα.

#5

Και εγώ θα ήθελα να δω, αν είναι εφικτό, έναν υπολογισμό του παραπάνω ολοκληρώματος με μεθόδους πραγματικής ανάλυσης...

BAGGP93 · #6

Γεια σου Γρηγόρη, γεια σου Τόλη, γεια σου

Μετά από δοκιμές και αντικαταστάσεις, υπολόγισα το ολοκλήρωμα με πραγματικές μεθόδους.

Έστω $\displaystyle{F(a,b)=\int_{0}^{\infty}\dfrac{\ln\,x}{(x+a)\,(x+b)}\,\mathrm{d}x\,\,,0<a<b}$ .

Θέτουμε $\displaystyle{x=\dfrac{1}{t}}$ , οπότε έχουμε

$\displaystyle{F(a,b)=-\int_{\infty}^{0}\dfrac{\ln(1/t)\,t^2}{(1+a\,t)\,(1+b\,t)}\,\dfrac{1}{t^2}\,\mathrm{d}t=\int_{0}^{\infty}\dfrac{-\ln\,x}{(a\,x+1)\,(b\,x+1)}\,\mathrm{d}x\,\,(I)}$

Απ' την άλλη,

$\displaystyle{\begin{aligned}F(a,b)&=\int_{0}^{\infty}\dfrac{\ln\,(a\,b)+\ln\,(x/(a\,b))}{a\,b\,\left(x/a+1\right)\,\left(x/b+1\right)}\,\mathrm{d}x\\&\stackrel{y=x/a\,b}{=}\int_{0}^{\infty}\dfrac{\ln\,(a\,b)+\ln\,x}{(a\,x+1)\,(b\,x+1)}\,\mathrm{d}x\,\,(II) \end{aligned}}$

Από τις σχέσεις $\displaystyle{(I)\,,(II)}$ παίρνουμε,

$\displaystyle{\begin{aligned}2\,F(a,b)&=\int_{0}^{\infty}\dfrac{\ln\,(a\,b)}{(a\,x+1)\,(b\,x+1)}\,\mathrm{d}x\\&=\ln\,(a\,b)\,\int_{0}^{\infty}\left(\dfrac{b}{b-a}\,\dfrac{1}{b\,x+1}-\dfrac{a}{b-a}\,\dfrac{1}{a\,x+1}\right)\,\mathrm{d}x\\&=\left[\dfrac{\ln\,(a\,b)}{b-a}\,\ln\,\left(\dfrac{b\,x+1}{a\,x+1}\right)\right]_{0}^{\infty}\\&=\dfrac{1}{b-a}\,\ln\,(a\,b)\,\ln\,(b/a) \end{aligned}}$

Ώστε, $\displaystyle{F(a,b)=\dfrac{1}{2\,(b-a)}\,\left(\ln^2\,b-\ln^2\,a\right)$

Tolaso J Kos · #7

BAGGP93 έγραψε: Ώστε, $\displaystyle{F(a,b)=\dfrac{1}{2\,(b-a)}\,\left(\ln^2\,b-\ln^2\,a\right)$

Tolaso J Kos · #8

Πώς περνάν τα χρόνια !!

Σεραφείμ , όπως πάντα, με Laplace !!

#9

Tolaso J Kos έγραψε:Πώς περνάν τα χρόνια !!

Σεραφείμ , όπως πάντα, με Laplace !!

Πωπω .. πριν 6 χρόνια .. πράγματι περνάνε. Ο Laplace βέβαια καλά κρατεί ..

#10

Σεραφείμ έγραψε:...Ο Laplace βέβαια καλά κρατεί ..

κι εμείς εδώ στο mathematica.gr κάτι κάνουμε Σεραφείμ...

Παρεμπιπτόντως, μήπως μπορούμε να βρούμε κάτι και για αυτήν την γενίκευση;

Tolaso J Kos · #11

grigkost έγραψε: ↑
Τετ Ιουν 07, 2017 1:14 pm
Για $0<\alpha<\beta$ , να υπολογισθεί το $\displaystyle\int_{0}^{+\infty}\frac{\log{x}}{(x+\alpha)(x+\beta)}\,dx\,.$

Μετά από τρία χρόνια ...! Μία άλλη λύση ... βλέπε και το θέμα εδώ.

Έστω r>0

και

. Κάνουμε την αντικατάσταση $t=\frac{ab}{x}$ . Τότε:

$\displaystyle{\begin{aligned} I_r &=\int_{a/r}^{rb}\frac{\ln(x) }{(x+a)(x+b)}\,\mathrm{d}x\\ &=\int_{rb}^{a/r}\frac{\ln \left ( \frac{ab}{t} \right ) }{(\frac{ab}{t}+a)(\frac{ab}{t}+b)}\cdot -\frac{ab}{t^2} \, \mathrm{d}t\\ &=\int_{a/r}^{rb}\frac{\ln \left ( \frac{ab}{t} \right ) }{(b+t)(a+t)}\,\mathrm{d}t\\ &=\ln (ab)\int_{a/r}^{rb}\frac{\mathrm{d}t}{(b+t)(a+t)}-I_r \end{aligned}}$
Οπότε,

$\displaystyle{\begin{aligned} I_r&=\frac{\ln (ab)}{2}\int_{a/r}^{rb}\frac{\mathrm{d}t}{(b+t)(a+t)}\\ &=\frac{\ln (ab)}{2(b-a)}\int_{a/r}^{rb}\left(\frac{1}{a+t}-\frac{1}{b+t}\right)\,\mathrm{d}t \\&=\frac{\ln (ab)}{2(b-a)}\left[\ln\left(\frac{a+t}{b+t}\right)\right]_{a/r}^{rb}\\ &= \frac{\ln (ab)}{2(b-a)}\ln\left(\frac{(a+rb)^2}{(1+r)^2ab}\right) \end{aligned}}$
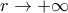Αφήνοντας το $r \rightarrow +\infty$ έχουμε πλέον ότι:

$\displaystyle{\mathbf{\int_0^{\infty} \frac{ \ln x }{(x+a)(x+b)} \, \mathrm{d}x=\frac{\ln^2 b-\ln^2 a }{2(b-a)}}}$

Γενικευμένο λογαριθμικό ολοκλήρωμα

Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Re: Γενικευμένο λογαριθμικό ολοκλήρωμα

Μέλη σε σύνδεση