![\mathcal{C} =[0, 1] \times [0, 1] \times \cdots \times[0, 1] \subseteq \mathbb{R}^n \mathcal{C} =[0, 1] \times [0, 1] \times \cdots \times[0, 1] \subseteq \mathbb{R}^n](/forum/ext/geomar/texintegr/latexrender/pictures/af4dfe5b3ef5cc47b76a5768d9cd6ba4.png) ο μοναδιαίος κύβος. Ορίζουμε τη συνάρτηση
ο μοναδιαίος κύβος. Ορίζουμε τη συνάρτηση όπου
όπου  θετικές σταθερές. Για ποιες τιμές των
θετικές σταθερές. Για ποιες τιμές των  είναι η τιμή του ολοκληρώματος
είναι η τιμή του ολοκληρώματος  πεπερασμένη ;
πεπερασμένη ;Άνευ λύσης!!
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
![\mathcal{C} =[0, 1] \times [0, 1] \times \cdots \times[0, 1] \subseteq \mathbb{R}^n \mathcal{C} =[0, 1] \times [0, 1] \times \cdots \times[0, 1] \subseteq \mathbb{R}^n](/forum/ext/geomar/texintegr/latexrender/pictures/af4dfe5b3ef5cc47b76a5768d9cd6ba4.png) ο μοναδιαίος κύβος. Ορίζουμε τη συνάρτηση
ο μοναδιαίος κύβος. Ορίζουμε τη συνάρτηση όπου
όπου  θετικές σταθερές. Για ποιες τιμές των
θετικές σταθερές. Για ποιες τιμές των  είναι η τιμή του ολοκληρώματος
είναι η τιμή του ολοκληρώματος  πεπερασμένη ;
πεπερασμένη ;
 , φαίνεται ότι το ολοκλήρωμα υπάρχει κατά Riemann,
, φαίνεται ότι το ολοκλήρωμα υπάρχει κατά Riemann,  .. (θέλει επεξεργασία .. θα δούμε ..)
.. (θέλει επεξεργασία .. θα δούμε ..)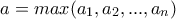

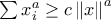

 (1)
(1)
 είναι η επιφάνεια της μοναδιαίας μπάλας και θέσουμε
είναι η επιφάνεια της μοναδιαίας μπάλας και θέσουμε 



 το ολοκλήρωμα συγκλίνει.
το ολοκλήρωμα συγκλίνει.

 , δηλαδή
, δηλαδή  .
. είναι συνεχής στο
είναι συνεχής στο  και
και  . Θέτουμε
. Θέτουμε  . Τότε
. Τότε 

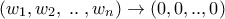 , με
, με  .
.

 προκύπτει ότι
προκύπτει ότι 
 τότε
τότε  , δηλαδή η
, δηλαδή η  , με συνεχή επέκταση
, με συνεχή επέκταση 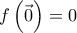 , γίνεται συνεχής και φραγμένη στο
, γίνεται συνεχής και φραγμένη στο  ,
, , τότε
, τότε  , που σημαίνει ότι δεν υπάρχει το
, που σημαίνει ότι δεν υπάρχει το  , καθότι
, καθότι  , όποια τιμή κι αν δώσουμε στο
, όποια τιμή κι αν δώσουμε στο  , επομένως ολοκληρώσιμη
, επομένως ολοκληρώσιμη  ).
). .
. συγκλίνει, παρόλο που
συγκλίνει, παρόλο που  και
και 

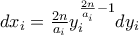









 δηλαδή
δηλαδή 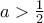



Καλημέρα Τόλη.Tolaso J Kos έγραψε:Πολύ ενδιαφέροντα όσα γράφετε. Σας ευχαριστώ.
Σταύρο,ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: Που την ψάρεψες αν θυμάσαι;









 τότε το ολοκλήρωμα πάνω στην επιφάνεια είναι πεπερασμένο γιατί
τότε το ολοκλήρωμα πάνω στην επιφάνεια είναι πεπερασμένο γιατί 




Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες