 όπου
όπου 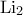 ο γνωστός διλογάριθμος.
ο γνωστός διλογάριθμος.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 όπου
όπου 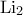 ο γνωστός διλογάριθμος.
ο γνωστός διλογάριθμος.
Tolaso J Kos έγραψε:Αποδείξατε ότι.
 τότε
τότε 

 , απ’ όπου προκύπτει το ζητούμενο.
, απ’ όπου προκύπτει το ζητούμενο. τότε
τότε  .. διότι .. ομοίως ..
.. διότι .. ομοίως ..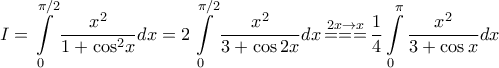

 , όπου
, όπου  οι ρίζες της
οι ρίζες της 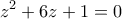
 , όπου
, όπου  ,
, 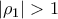 και
και 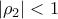


 , καθώς και
, καθώς και  έχουμε
έχουμε 


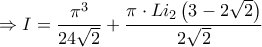
Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 6 επισκέπτες