![\displaystyle{a \in \left( {0,1} \right]} \displaystyle{a \in \left( {0,1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/be0d50f0b5604e981980cd97412153a7.png) να δειχθεί ότι
να δειχθεί ότι  .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
Σεραφείμ,Σεραφείμ έγραψε:Αννα δειχθεί ότι
.
 ; Με το λίγο που το έτρεξα στο Wolfram μου δίνει ότι αποκλίνει εκτός της τιμής
; Με το λίγο που το έτρεξα στο Wolfram μου δίνει ότι αποκλίνει εκτός της τιμής  ... Παλαιότερα πάντως είχαμε δει έναν Τριλογάριθμο ....
... Παλαιότερα πάντως είχαμε δει έναν Τριλογάριθμο ....
 Όμως ο τριλογάριθμος ικανοποιεί τη σχέση
Όμως ο τριλογάριθμος ικανοποιεί τη σχέση Θέτουμε στη προηγούμενη σχέση
Θέτουμε στη προηγούμενη σχέση 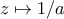 και άρα
και άρα Άρα
Άρα![\displaystyle{\boxed{\color{blue}{\int_{0}^{1} \frac{\log^2 x}{x+a} \, {\rm d}x = -2 {\rm Li}_3 \left ( -a \right )- \frac{\log^3 a}{3} - \frac{\pi^2 \log a}{3}}\quad , \quad a \in (0, 1]} } \displaystyle{\boxed{\color{blue}{\int_{0}^{1} \frac{\log^2 x}{x+a} \, {\rm d}x = -2 {\rm Li}_3 \left ( -a \right )- \frac{\log^3 a}{3} - \frac{\pi^2 \log a}{3}}\quad , \quad a \in (0, 1]} }](/forum/ext/geomar/texintegr/latexrender/pictures/e43815335791b81dd64e8bdbd9fe5709.png)

Tolaso J Kos έγραψε:Σεραφείμ,Σεραφείμ έγραψε:Αννα δειχθεί ότι
.
είναι σίγουρο ότι συγκλίνει για τις τιμές του; Με το λίγο που το έτρεξα στο Wolfram μου δίνει ότι αποκλίνει εκτός της τιμής
... Παλαιότερα πάντως είχαμε δει έναν Τριλογάριθμο ....
 το ολοκλήρωμα αποκλίνει.
το ολοκλήρωμα αποκλίνει.
Λόγω αυτού https://en.wikipedia.org/wiki/Hilbert_transformTolaso J Kos έγραψε:Σταύρο ευχαριστώ. Έδωσα , πιο πάνω , και τη σωστή θεωρώ εκδοχή !!

 .
.Χμμ.. δε το γνωρίζω αυτό.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:
Λόγω αυτού https://en.wikipedia.org/wiki/Hilbert_transform

Τόλη, και με "+" στην θέση του "-" έχουμε πρόβλημα.Tolaso J Kos έγραψε: Έδωσα , πιο πάνω , και τη σωστή θεωρώ εκδοχή !!
αποκλίνει για ολόκληρο διάστημαTolaso J Kos έγραψε: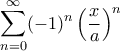
 , πόσο μάλλον ότι η εναλλαγή αθροίσματος και ολοκλήρωσης είναι μη επιτρεπτή.
, πόσο μάλλον ότι η εναλλαγή αθροίσματος και ολοκλήρωσης είναι μη επιτρεπτή.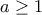 . Τώρα η σειρά συγκλίνει και επιτρέπεται η εναλλαγή ολοκλήρωσης και άθροισης και βγάζουμε το ίδιο αποτέλεσμα. Στη συνέχεια για να ρθουμε πίσω στο
. Τώρα η σειρά συγκλίνει και επιτρέπεται η εναλλαγή ολοκλήρωσης και άθροισης και βγάζουμε το ίδιο αποτέλεσμα. Στη συνέχεια για να ρθουμε πίσω στο ![a \in (0, 1] a \in (0, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/45e3cd0bf215d66be6aa4e9c8a0c6caa.png) μπορούμε να χρησιμοποιήσουμε την αναλυτική συνέχεια της πολυλογαρίθμου και έτσι το αποτέλεσμα να ισχύει και για αυτά τα
μπορούμε να χρησιμοποιήσουμε την αναλυτική συνέχεια της πολυλογαρίθμου και έτσι το αποτέλεσμα να ισχύει και για αυτά τα  .
.
 , και
, και  να αποδειχθεί ότι
να αποδειχθεί ότι 
 ορίζεται στο
ορίζεται στο 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 10 επισκέπτες