 του
του  έχει μηδενικό μέτρο και είναι Jordan-μετρήσιμο, τότε
έχει μηδενικό μέτρο και είναι Jordan-μετρήσιμο, τότε  .
.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 του
του  έχει μηδενικό μέτρο και είναι Jordan-μετρήσιμο, τότε
έχει μηδενικό μέτρο και είναι Jordan-μετρήσιμο, τότε  .
.
 και
και  Jordan μετρήσιμο
Jordan μετρήσιμο  το ολοκλήρωμα
το ολοκλήρωμα  είναι καλά ορισμένο. Επίσης
είναι καλά ορισμένο. Επίσης  υπάρχει ακολουθία
υπάρχει ακολουθία  κλειστών ορθογωνίων του
κλειστών ορθογωνίων του 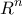 ώστε
ώστε  και
και  , όπου
, όπου  ο όγκος του ορθογωνίου
ο όγκος του ορθογωνίου  .
. 
 . Επειδή το
. Επειδή το  είναι Jordan-μετρήσιμο για κάθε ορθογώνιο
είναι Jordan-μετρήσιμο για κάθε ορθογώνιο 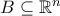 με
με  , ισχύει
, ισχύει
 Όμως το
Όμως το  είναι και μηδενικού μέτρου. Επομένως για
είναι και μηδενικού μέτρου. Επομένως για  υπάρχει συλλογή
υπάρχει συλλογή 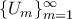 (*) κλειστών ορθογωνίων τέτοια ώστε
(*) κλειστών ορθογωνίων τέτοια ώστε  και
και
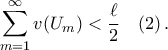
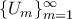 με μια συλλογή ορθογωνίων
με μια συλλογή ορθογωνίων  , έτσι ώστε
, έτσι ώστε 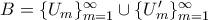 , παρατηρούμε ότι για
, παρατηρούμε ότι για  ισχύει
ισχύει 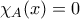 .
.  προκύπτει
προκύπτει
 Άτοπο. Άρα
Άτοπο. Άρα  .
. υπάρχει τουλάχιστον ένα σημείο του
υπάρχει τουλάχιστον ένα σημείο του  . Επομένως για
. Επομένως για 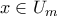 ισχύει
ισχύει  .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες