Ελάχιστη τιμή δεύτερης παραγώγου

AlexandrosG · #1

Έστω $f\in C^2([0,1])$ . Να δείξετε ότι

$\displaystyle{8 \, (\max f-\min f) \geq \min f''}$

Την είδα στο AoPS και μου άρεσε πολύ.

#2

Η ανάρτηση αποσύρεται ως λανθασμένη. Ευχαριστώ τον Σταύρο που το πρόσεξε.

ΕΜΦΑΝΙΣΗ ΚΕΙΜΕΝΟΥ

#3

Επανέρχομαι με μια σωστή αυτή την φορά (ελπίζω) λύση.

Έστω $\min f'' = k$ . Μπορώ να υποθέσω ότι k > 0

αφού σε αντίθετη περίπτωση το ζητούμενο είναι άμεσο. Άρα η

είναι κυρτή.

Περίπτωση 1: Το ελάχιστο της

εμφανίζεται σε σημείο $a \in (0,1)$ . Τότε το

είναι τοπικό ελάχιστο και άρα f'(a) = 0

. Από θεώρημα Taylor έχουμε

$\displaystyle f(x) = f(a) + f'(a)(x-a) + f''(t)(x-a)^2/2$

για κάποιο

μεταξύ του

και του

.

Χωρίς βλάβη της γενικότητας είναι $a \leqslant 1/2$ . Τότε

$\displaystyle \displaystyle{f(1) = f(a) + f'(a)(x-a) + f''(t)(x-a)^2/2 = f(a) + f''(t)(x-a)^2/2 \geqslant f(a) + \frac{k(1/2)^2}{2} = f(a) + k/8}$

Άρα $\min f'' = k \leqslant 8(f(1) - f(a)) \leqslant 8(\max f - \min f)$ .

Περίπτωση 2: Το ελάχιστο της

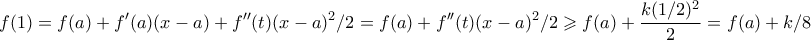
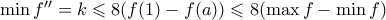εμφανίζεται σε άκρο, έστω στο

. Η

είναι κυρτή, άρα θα είναι αύξουσα και το μέγιστό της θα εμφανίζεται στο

. Από Taylor στο [1/2,1]

έχω

$\displaystyle f(1) = f(1/2) + \frac{f'(1/2)}{2} + \frac{f''(t)}{8}$

για κάποιο $t \in (1/2,1)$ . Επειδή $f'(1/2) \geqslant 0$ , καταλήγω στο συμπέρασμα όπως προηγουμένως.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #4

Να σημειώσω ότι η λύση του Δημήτρη δεν χρησιμοποιεί την συνέχεια της δεύτερης παραγώγου.

Η εκφώνηση σε αυτή την περίπτωση θα ήταν

$8(maxf-minf)\geq inf f''$

και θα χρειαζόταν μόνο η ύπαρξη της δεύτερης παραγώγου.

Για το θέμα υπάρχει λύση κάνοντας ολοκληρώσεις.
Εκεί χρειάζεται η συνέχεια της δεύτερης παραγώγου.

Ελάχιστη τιμή δεύτερης παραγώγου

Ελάχιστη τιμή δεύτερης παραγώγου

Re: Ελάχιστη τιμή δεύτερης παραγώγου

Re: Ελάχιστη τιμή δεύτερης παραγώγου

Re: Ελάχιστη τιμή δεύτερης παραγώγου

Μέλη σε σύνδεση