Όριο πάλι...

M.S.Vovos · #1

Έστω ο μη αρνητικός πραγματικός

. Να υπολογίσετε το όριο:

$\displaystyle{\lim_{n\rightarrow \infty }\displaystyle n^{-\frac{1}{p+1}}\left (\prod_{k=1}^{n}k^{k^{p}} \right )^{\displaystyle \frac{1}{n^{p+1}}}}$
Φιλικά,
Μάριος

dement · #2

Παίρνουμε τον λογάριθμο της παράστασης, ο οποίος είναι

$\displaystyle - \frac{1}{p+1} \ln n + \frac{1}{n^{p+1}} \sum_{k=1}^n k^p \ln k = \frac{1}{n} \sum_{k=1}^n \left( \frac{k}{n} \right)^p \ln \left( \frac{k}{n} \right) + \ln n \cdot \left( \frac{1}{n} \sum_{k=1}^n \left( \frac{k}{n} \right)^p - \frac{1}{p+1} \right) =$

$\displaystyle = \frac{1}{n} \sum_{k=1}^n \left( \frac{k}{n} \right)^p \ln \left( \frac{k}{n} \right) + \ln n \cdot \left( \frac{1}{n} \sum_{k=1}^n \left( \frac{k}{n} \right)^p - \int_0^1 x^p \mathrm{d}x \right)$

Η x^p

είναι Lipschitz αν $p \geqslant 1$ ενώ είναι

-Hoelder συνεχής στο [0,1]

αν

. Στην πρώτη περίπτωση, ο δεύτερος όρος τείνει στο

ως $\displaystyle \mathcal{O} \left( \frac{\ln n}{n} \right)$ ενώ στη δεύτερη ως $\displaystyle \mathcal{O} \left( \frac{\ln n}{n^p} \right)$ . Αν p=0

τότε βέβαια ο δεύτερος όρος είναι σταθερά

.

Έτσι, μας μένει ο πρώτος όρος ο οποίος είναι άθροισμα Riemann, οπότε τείνει στο ολοκλήρωμα $\displaystyle \int_0^1 x^p \ln x \mathrm{d} x = - \frac{1}{(p+1)^2}$ . Τελικά, το όριο είναι $\displaystyle \mathrm{e}^{- \frac{1}{(p+1)^2}}$ .

Tolaso J Kos · #3

Έκανα ακριβώς τα ίδια εχθές αλλά έκανα λάθος στις εκτιμήσεις... μου φυγαν κάποιοι όροι και έβρισκα αποτελέσματα ό, τι να 'ναι !! Σήμερα το πρωί που το κοίταξα είδα τα λάθη και βρήκα τελικά το όριο.

Ευχάριστο παίδεμα ήταν. Μάριε ευχαριστώ.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #4

Θα υπολογισθεί το όριο για $p\neq -1$

Ο λογάριθμος της παράστασης είναι

$\displaystyle - \frac{1}{p+1} \ln n + \frac{1}{n^{p+1}} \sum_{k=1}^n k^p \ln k }$

Αν p< -1

τότε βλέπουμε ότι το όριο του λογαρίθμου είναι $\infty$
οπότε και το όριο της ακολουθίας.

Οι περιπτώσεις -1<p<0,

και $p\geq 0$ είναι λίγο διαφορετικές.

Εστω $p\geq 0$

Το βασικό στοιχείο είναι ότι αν $f:[1,\infty )\rightarrow \mathbb{R}$ είναι μη αρνητική και αύξουσα τότε

$-f(n)\leq \int_{1}^{n}f(x)dx-\sum_{k=1}^{n}f(k)\leq- f(1)$ (1)

Αν το εφαρμόσουμε στην $f(x)=x^{p}lnx$ για p>0

παίρνουμε

$-n^p \ln n\leq \int_{1}^{n}x^p \ln xdx -\sum_{k=1}^n k^p \ln k } \leq 0$

Αλλά $\int_{1}^{n}x^p \ln xdx=\frac{n^{p+1}}{p+1}\ln n-\frac{n^{p+1}}{(p+1)^{2}}+\frac{1}{(p+1)^{2}}$

Αντικαθιστώντας παίρνουμε ότι το όριο του λογαρίθμου της παράστασης είναι $-\frac{1}{(p+1)^{2}}$

Για p=0

κάνουμε τα ίδια για την f(x)=lnx

παίρνουμε ότι το όριο του λογαρίθμου της παράστασης είναι

.

Για

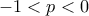θέλουμε ένα ανάλογο της (1) για συνάρτηση τελικά φθίνουσα.

Το όριο πάλι προκύπτει ότι είναι $-\frac{1}{(p+1)^{2}}$ .

Να ζητήσω προκαταβολικά συγνώμη για την παράληψη απόδειξης της τελευταίας περίπτωσης
καθώς και λεπτομερειών για τις άλλες.

Συμπλήρωμα.Διορθώθηκε τυπογραφικό στην σχέση (1)

M.S.Vovos · #5

Σταύρο καλησπέρα. Μπορείς να δώσεις την απόδειξη για την σχέση (1);

Ευχαριστώ.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #6

M.S.Vovos έγραψε: ↑
Πέμ Φεβ 22, 2018 11:25 pm
Σταύρο καλησπέρα. Μπορείς να δώσεις την απόδειξη για την σχέση (1);

Ευχαριστώ.

Καλημέρα Μάριε.

Υπάρχει τυπογραφικό στην (1) που βέβαια το διόρθωσα.

Η σωστή είναι
$-f(n)\leq \int_{1}^{n}f(x)dx-\sum_{k=1}^{n}f(k)\leq- f(1)$ (1).

Αποδεικνύεται ως εξής

Αφου η συνάρτηση είναι αύξουσα προφανώς είναι

$f(k)\leq \int_{k}^{k+1}f(x)dx\leq f(k+1)$

Αθροίζοντας από

έως

παίρνουμε

$\sum_{k=1}^{n-1}f(k)\leq \int_{1}^{n}f(x)dx\leq \sum_{k=2}^{n}f(k)$

προσθαφερόντας τα f(n),f(1)

στο αριστερό δεξιό μέλος αντίστοιχα παίρνουμε την (1).

Εγώ πάντως για να την δω κάνω ένα σχήμα.

Όριο πάλι...

Όριο πάλι...

Re: Όριο πάλι...

Re: Όριο πάλι...

Re: Όριο πάλι...

Re: Όριο πάλι...

Re: Όριο πάλι...

Μέλη σε σύνδεση