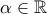 για τους οποία η παρακάτω σειρά έχει νόημα να δειχθεί ότι:
για τους οποία η παρακάτω σειρά έχει νόημα να δειχθεί ότι:![\displaystyle{\sum_{n=1}^{\infty} \frac{n \coth n \pi}{n^4 -\alpha^4} = \frac{1}{4\alpha^2 \pi} \left [ \frac{1}{\alpha^2} - \pi^2 \cot \pi \alpha \coth \pi \alpha \right ]} \displaystyle{\sum_{n=1}^{\infty} \frac{n \coth n \pi}{n^4 -\alpha^4} = \frac{1}{4\alpha^2 \pi} \left [ \frac{1}{\alpha^2} - \pi^2 \cot \pi \alpha \coth \pi \alpha \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/3bc8110738a4b7e747f2375cc9fbe614.png)
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
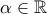 για τους οποία η παρακάτω σειρά έχει νόημα να δειχθεί ότι:
για τους οποία η παρακάτω σειρά έχει νόημα να δειχθεί ότι:![\displaystyle{\sum_{n=1}^{\infty} \frac{n \coth n \pi}{n^4 -\alpha^4} = \frac{1}{4\alpha^2 \pi} \left [ \frac{1}{\alpha^2} - \pi^2 \cot \pi \alpha \coth \pi \alpha \right ]} \displaystyle{\sum_{n=1}^{\infty} \frac{n \coth n \pi}{n^4 -\alpha^4} = \frac{1}{4\alpha^2 \pi} \left [ \frac{1}{\alpha^2} - \pi^2 \cot \pi \alpha \coth \pi \alpha \right ]}](/forum/ext/geomar/texintegr/latexrender/pictures/3bc8110738a4b7e747f2375cc9fbe614.png)

 (βλέποντας και την τελική απάντηση).
(βλέποντας και την τελική απάντηση). με
με  . Αυτή έχει:
. Αυτή έχει: (πράσινα σημεία), με υπόλοιπο
(πράσινα σημεία), με υπόλοιπο  .
.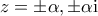 (μπλε σημεία), όλους με υπόλοιπο
(μπλε σημεία), όλους με υπόλοιπο  .
. (κόκκινο σημείο) με υπόλοιπο
(κόκκινο σημείο) με υπόλοιπο  .
. όπου
όπου 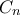 το μαύρο τετράγωνο (μεταξύ των σημείων
το μαύρο τετράγωνο (μεταξύ των σημείων  ). Ισχύει (για αρκετά μεγάλο
). Ισχύει (για αρκετά μεγάλο  ώστε τα μπλε σημεία να πέφτουν μέσα στο τετράγωνο)
ώστε τα μπλε σημεία να πέφτουν μέσα στο τετράγωνο)  . Αφού όμως η συνεφαπτομένη είναι φραγμένη στο
. Αφού όμως η συνεφαπτομένη είναι φραγμένη στο  , ισχύει
, ισχύει  , από όπου προκύπτει το ζητούμενο.
, από όπου προκύπτει το ζητούμενο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες