 ακολουθία τέτοια ώστε
ακολουθία τέτοια ώστε  και
και  . Να δειχθεί ότι το όριο
. Να δειχθεί ότι το όριο  δεν υπάρχει.
δεν υπάρχει.Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 ακολουθία τέτοια ώστε
ακολουθία τέτοια ώστε  και
και  . Να δειχθεί ότι το όριο
. Να δειχθεί ότι το όριο  δεν υπάρχει.
δεν υπάρχει.
ΘέτουμεTolaso J Kos έγραψε: ↑Παρ Μαρ 08, 2024 9:48 pmΈστωακολουθία τέτοια ώστε
και
. Να δειχθεί ότι το όριο
δεν υπάρχει.
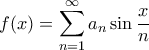 , η οποία συγκλίνει από το M-test του Weierstrass.
, η οποία συγκλίνει από το M-test του Weierstrass. 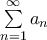 είναι ο
είναι ο  .
.  τέτοιο ώστε για κάθε
τέτοιο ώστε για κάθε 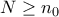 να ισχύει
να ισχύει 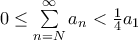 .
. 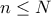 τότε το
τότε το  διαιρεί το
διαιρεί το  και άρα
και άρα 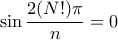 έχουμε
έχουμε 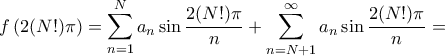
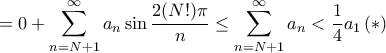
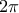 περιοδικότητα της
περιοδικότητα της  ότι
ότι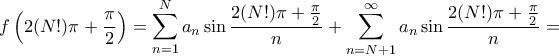
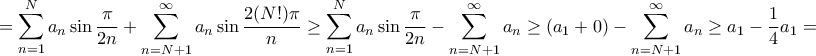
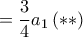
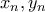 που τείνουν στο άπειρο αλλά για τις οποίες είδαμε στις
που τείνουν στο άπειρο αλλά για τις οποίες είδαμε στις 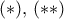 ότι
ότι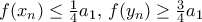 . Έπεται ότι το
. Έπεται ότι το 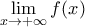 δεν υπάρχει.
δεν υπάρχει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες