Πάντα είχα ένα προβληματισμό από ποια σημεία του επιπέδου μπορούμε να φέρουμε εφαπτόμενες στην υπερβολή
 .
. Η αντιμετώπιση μάλλον ξεφεύγει από τις γνώσεις της Β Λυκείου και γίνεται ένα ενδιαφέρον θέμα στην Γ Λυκείου πιστεύω.
Έτσι λύνοντας ως προς
 έχουμε ότι
έχουμε ότι ![y=\pm \frac{\beta }{\alpha }\sqrt{{{x}^{2}}-{{\alpha }^{2}}},\,\,x\in (-\infty ,\,\,-\alpha ]\cup [\alpha ,\,\,+\infty ) y=\pm \frac{\beta }{\alpha }\sqrt{{{x}^{2}}-{{\alpha }^{2}}},\,\,x\in (-\infty ,\,\,-\alpha ]\cup [\alpha ,\,\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/ff67f464eaa05e8742d7a28e46d101f8.png)
Θεωρώντας την συνάρτηση
![f(x)=\frac{\beta }{\alpha }\sqrt{{{x}^{2}}-{{\alpha }^{2}}},\,\,x\in (-\infty ,\,\,-\alpha ]\cup [\alpha ,\,\,+\infty ) f(x)=\frac{\beta }{\alpha }\sqrt{{{x}^{2}}-{{\alpha }^{2}}},\,\,x\in (-\infty ,\,\,-\alpha ]\cup [\alpha ,\,\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/092f6c2dba521d26169b67295b736386.png)
δηλαδή τους δύο κλάδους πάνω από τον
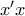 , είναι παραγωγίσιμη στο
, είναι παραγωγίσιμη στο  με
με  ή
ή  (1).
(1).Αν
 τυχαίο σημείο του επιπέδου, θέλουμε την εφαπτόμενη της
τυχαίο σημείο του επιπέδου, θέλουμε την εφαπτόμενη της  στο
στο  με εξίσωση
με εξίσωση 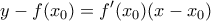 να περνά από το σημείο
να περνά από το σημείο  άρα να ισχύει ότι
άρα να ισχύει ότι  . Επομένως αναζητούμε πόσες ρίζες έχει η εξίσωση
. Επομένως αναζητούμε πόσες ρίζες έχει η εξίσωση 
στο σύνολο

Γι αυτό θεωρώντας την συνάρτηση

είναι παραγωγίσιμη στο
 με
με 
και επειδή η
 (…εύκολα αποδεικνύετε άλλωστε η υπερβολή είναι κοίλη…)
(…εύκολα αποδεικνύετε άλλωστε η υπερβολή είναι κοίλη…) έχουμε ότι για
 και για
και για 
1)Αν
 δηλαδή το σημείο
δηλαδή το σημείο  βρίσκεται μέσα στην ταινία των κατακόρυφων εφαπτόμενων
βρίσκεται μέσα στην ταινία των κατακόρυφων εφαπτόμενων  η
η  είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο  και γνήσια αύξουσα στο
και γνήσια αύξουσα στο  και τότε
και τότε 
και επειδή
 και
και 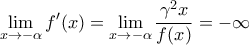
(λόγω της (1) είναι
 ) και
) και  είναι
είναι  και επειδή είναι
και επειδή είναι 

είναι
 και τότε:
και τότε:αν
 δηλαδή το σημείο
δηλαδή το σημείο  είναι πάνω από την
είναι πάνω από την ασύμπτωτη
 το
το  και τότε η
και τότε η  δεν έχει ρίζα
δεν έχει ρίζα και αν
 (κάτω από την ασύμπτωτη ) το
(κάτω από την ασύμπτωτη ) το 
και τότε η
 έχει μοναδική ρίζα λόγω μονοτονίας.
έχει μοναδική ρίζα λόγω μονοτονίας.Για το
 αφού
αφού  γνήσια αύξουσα θα είναι
γνήσια αύξουσα θα είναι  (…υπολογίζοντας τα όρια όπως πριν..) και τότε :
(…υπολογίζοντας τα όρια όπως πριν..) και τότε : αν
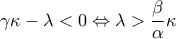 δηλαδή το σημείο
δηλαδή το σημείο  είναι πάνω από την
είναι πάνω από την ασύμπτωτη
 το
το 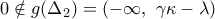 και τότε η
και τότε η  δεν έχει ρίζα
δεν έχει ρίζακαι αν
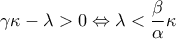 (κάτω από την ασύμπτωτη..) το
(κάτω από την ασύμπτωτη..) το 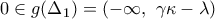 και τότε η
και τότε η  έχει μοναδική ρίζα λόγω μονοτονίας.
έχει μοναδική ρίζα λόγω μονοτονίας. Βγάζοντας συμπέρασμα όταν το σημείο
 βρίσκεται μέσα στην ταινία των κατακόρυφων εφαπτόμενων
βρίσκεται μέσα στην ταινία των κατακόρυφων εφαπτόμενων  και πάνω από τις ασύμπτωτες της καμπύλης δεν υπάρχει έχουμε καμμία εφαπτομένη,
και πάνω από τις ασύμπτωτες της καμπύλης δεν υπάρχει έχουμε καμμία εφαπτομένη, όταν βρίσκεται ανάμεσα στις ασύμπτωτες μία εφαπτομένη και όταν είναι κάτω από τις ασύμπτωτες δύο.
2) Αν
 ή
ή  δηλαδή το σημείο
δηλαδή το σημείο  βρίσκεται σε μία από τις κατακόρυφες εφαπτόμενες
βρίσκεται σε μία από τις κατακόρυφες εφαπτόμενες  η
η όπως προηγούμενα
όπως προηγούμενα 3) Αν
 (δηλαδή το σημείο βρίσκεται έξω από την ταινία στο δεξιά κλάδο) έχοντας ότι για
(δηλαδή το σημείο βρίσκεται έξω από την ταινία στο δεξιά κλάδο) έχοντας ότι για  και για
και για  η
η  είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο 
και στο διάστημα
![\displaystyle{{{\Alpha }_{1}}=(\alpha ,\,\,\kappa ]} \displaystyle{{{\Alpha }_{1}}=(\alpha ,\,\,\kappa ]}](/forum/ext/geomar/texintegr/latexrender/pictures/7c7fd6d2a0fa75e621fe949783a87a3b.png) και γνήσια αύξουσα στο διάστημα
και γνήσια αύξουσα στο διάστημα 
Τώρα για το
 είναι
είναι  και όπως στο (1) οι περιπτώσεις.
και όπως στο (1) οι περιπτώσεις.Τώρα για
 η
η  παρουσιάζει ελάχιστο στο
παρουσιάζει ελάχιστο στο  το
το  και επειδή
και επειδή  έχουμε ότι
έχουμε ότι  και
και  οπότε:
οπότε:Αν
 προφανώς έχουμε μοναδική ρίζα και άρα μοναδική εφαπτομένη.
προφανώς έχουμε μοναδική ρίζα και άρα μοναδική εφαπτομένη.Αν
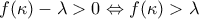 δηλαδή το σημείο βρίσκεται στα κοίλα της καμπύλης του δεξιού κλάδου), καμία εφαπτομένη.
δηλαδή το σημείο βρίσκεται στα κοίλα της καμπύλης του δεξιού κλάδου), καμία εφαπτομένη.Αν
 τότε έχει μία ρίζα στο
τότε έχει μία ρίζα στο  και επιπλέον
και επιπλέον Αν
 δηλαδή το σημείο βρίσκεται πάνω από την ασύμπτωτη
δηλαδή το σημείο βρίσκεται πάνω από την ασύμπτωτη  δεν έχει άλλη ρίζα και αν
δεν έχει άλλη ρίζα και αν 
τότε έχει και άλλη ρίζα στο διάστημα

δηλαδή όταν είναι το σημείο μεταξύ της ασύμπτωτης και της καμπύλης έξω από το ορθογώνιο βάσης έχουμε δύο εφαπτόμενες!!!)
4) Αν
 (δηλαδή το σημείο βρίσκεται έξω από την ταινία στο αριστερά κλάδο) έχοντας ότι για
(δηλαδή το σημείο βρίσκεται έξω από την ταινία στο αριστερά κλάδο) έχοντας ότι για  και για
και για  η
η  είναι γνήσια φθίνουσα στο
είναι γνήσια φθίνουσα στο ![\displaystyle{(-\infty ,\,\,\kappa ]} \displaystyle{(-\infty ,\,\,\kappa ]}](/forum/ext/geomar/texintegr/latexrender/pictures/caff5409cd546739c86e72f2606652d5.png)
και γνήσια αύξουσα στο διάστημα
 και γνήσια αύξουσα στο διάστημα
και γνήσια αύξουσα στο διάστημα  .
. Ανάλογα συμβαίνουν τώρα για τις ρίζες όπως στην προηγούμενη διερεύνηση.
Θα προσπαθήασω να το εμφανίσω και με σχήμα...
Φιλικά και Μαθηματικά
Βασίλης

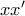 .
. .
.