 και
και  .
.Πώς θα αποδείξουμε ότι
 ;
;Συντονιστής: Παύλος Μαραγκουδάκης
Κάνω μία άχαρη λύση, πιο πολύ για επιβεβαίωση, εν αναμονή κομψού συλλογισμού.
 . Αρκεί η
. Αρκεί η  και άρα, πολλαπλασιάζοντας επί
και άρα, πολλαπλασιάζοντας επί  έχουμε ισοδύναμα
έχουμε ισοδύναμα  ή αλλιώς
ή αλλιώς  , οπότε αρκεί να δείξουμε ότι
, οπότε αρκεί να δείξουμε ότι  .
.  οπότε ισοδύναμα
οπότε ισοδύναμα  , οπότε θέλουμε
, οπότε θέλουμε  .
.  , που επιβεβαιώνει το αποδεικτέο.
, που επιβεβαιώνει το αποδεικτέο. .
. και υπολογίσουμε τα αντίστοιχα αθροίσματα, δε θα βγάλουμε άκρη, γιατί , σύμφωνα με λογισμικό, η ελάχιστη τιμή του
και υπολογίσουμε τα αντίστοιχα αθροίσματα, δε θα βγάλουμε άκρη, γιατί , σύμφωνα με λογισμικό, η ελάχιστη τιμή του  , ώστε να πάρουμε άθροισμα μεγαλύτερο του
, ώστε να πάρουμε άθροισμα μεγαλύτερο του  , είναι
, είναι  .
. και έχουμε από Cauchy Schwartz:
και έχουμε από Cauchy Schwartz:![\sum_{i=1}^{n}\dfrac{1}{n+i}=\sum_{i=0}^{k-1}\sum_{j=1}^{m}\dfrac{1}{(k+i)m+j}> \sum_{i=0}^{k-1}\dfrac{m^2}{\frac{(k+i+1)m[(k+i+1)m+1]}{2}-\frac{(k+i)m[(k+i)m+1]}{2}}= \sum_{i=1}^{n}\dfrac{1}{n+i}=\sum_{i=0}^{k-1}\sum_{j=1}^{m}\dfrac{1}{(k+i)m+j}> \sum_{i=0}^{k-1}\dfrac{m^2}{\frac{(k+i+1)m[(k+i+1)m+1]}{2}-\frac{(k+i)m[(k+i)m+1]}{2}}=](/forum/ext/geomar/texintegr/latexrender/pictures/091ebfc4d71ef421b10d23c01c529178.png)
 .
. .
.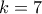 , αρκεί να δείξουμε ότι:
, αρκεί να δείξουμε ότι: ,
,  γράφεται ως συνεχές κλάσμα ως:
γράφεται ως συνεχές κλάσμα ως: , που είναι μεγαλύτερο από:
, που είναι μεγαλύτερο από: .
. και
και  παίρνουμε:
παίρνουμε: θετικοί όροι.
θετικοί όροι.  και πετάμε τους θετικούς όρους. Έτσι, παίρνουμε μια προσέγγιση (με έλλειμα) του
και πετάμε τους θετικούς όρους. Έτσι, παίρνουμε μια προσέγγιση (με έλλειμα) του 
 .
. Θαυμάσια.Λάμπρος Κατσάπας έγραψε: ↑Τετ Δεκ 27, 2023 6:47 pmΣυνδυάζοντας τα αναπτύγματα MacLaurin τωνκαι
παίρνουμε:
θετικοί όροι.
Θέτουμεκαι πετάμε τους θετικούς όρους. Έτσι, παίρνουμε μια προσέγγιση (με έλλειμα) του

Συγκεκριμένα,.
Εύκολα ελέγχουμε ότι αυτή η προσέγγιση είναι πολύ καλύτερη από αυτή που ζητείται.
 για
για  (υπάρχουν πολλές αποδείξεις. Μία είναι από το γεγονός ότι έχουμε άθροισμα γεωμετρικής προόδου
(υπάρχουν πολλές αποδείξεις. Μία είναι από το γεγονός ότι έχουμε άθροισμα γεωμετρικής προόδου  , και λοιπά.)
, και λοιπά.) έως
έως  , και προκύπτει η ανισότητα του Λάμπρου.
, και προκύπτει η ανισότητα του Λάμπρου.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες