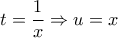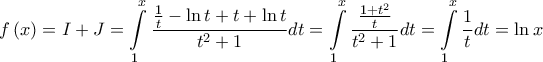.
.Δίνονται οι συναρτήσεις:

 με
με 

 με
με  και
και
 ορισμένη και παραγωγίσιμη στο
ορισμένη και παραγωγίσιμη στο  με
με  για την οποία ισχύει ότι
για την οποία ισχύει ότι ![\displaystyle{e^{x+h(x)}[1+xh'(x)] + {{e}^{1+{{e}^{-x }}}}= 0 \,\,, x>0} \displaystyle{e^{x+h(x)}[1+xh'(x)] + {{e}^{1+{{e}^{-x }}}}= 0 \,\,, x>0}](/forum/ext/geomar/texintegr/latexrender/pictures/6f877d1190174b6ca4e50ed7544add50.png) .
.α) Να βρείτε τις συναρτήσεις
 και
και 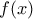
β) Να υπολογίσετε το εμβαδόν του χωρίου που περικλείεται από τη γραφική παράσταση της συνάρτησης
 , τον άξονα
, τον άξονα  και την ευθεία
και την ευθεία 
γ) Να αποδείξετε ότι
 για κάθε
για κάθε 
δ) Να μελετήσετε τη συνάρτηση
 ως προς τη μονοτονία
ως προς τη μονοτονίαε) Να υπολογίσετε το όριο

στ) Να αποδείξετε ότι

ζ) Να βρείτε το σύνολο τιμών της συνάρτησης

η) Να λύσετε την εξίσωση





 με παραγοντική ολοκλήρωση .
με παραγοντική ολοκλήρωση .![g(x)=f(e^{x}-1)-f(x)>0/tex] γιατί η f \nearrow x>0, e^{x}-1>x,x>0\Rightarrow f(e^{x}-1)>f(x)\Rightarrow g>0 g(x)=f(e^{x}-1)-f(x)>0/tex] γιατί η f \nearrow x>0, e^{x}-1>x,x>0\Rightarrow f(e^{x}-1)>f(x)\Rightarrow g>0](/forum/ext/geomar/texintegr/latexrender/pictures/068377e6bfc3bb9abf5146a2e7a8f250.png)
 γιατί
γιατί









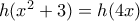 ,αφου
,αφου 
 οι λύσεις
οι λύσεις
 θέτουμε
θέτουμε  οπότε
οπότε 
 ,
,