 με
με  για τους οποίους ισχύει
για τους οποίους ισχύει ,
, 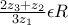 και ο
και ο  δεν είναι πραγματικός αριθμός. Να αποδείξετε ότι
δεν είναι πραγματικός αριθμός. Να αποδείξετε ότι 
Συντονιστής: Πρωτοπαπάς Λευτέρης
 με
με  για τους οποίους ισχύει
για τους οποίους ισχύει ,
, 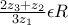 και ο
και ο  δεν είναι πραγματικός αριθμός. Να αποδείξετε ότι
δεν είναι πραγματικός αριθμός. Να αποδείξετε ότι 
Εξ υποθέσεως υπάρχουνthanasis kopadis έγραψε:Δίνονται οι μιγαδικοί αριθμοίμε
για τους οποίους ισχύει
,
και ο
δεν είναι πραγματικός αριθμός. Να αποδείξετε ότι
 με
με  . Πολλαπλασιάζοντας την δεύτερη επί
. Πολλαπλασιάζοντας την δεύτερη επί  και αφαιρώντας κατά μέλη έπεται
και αφαιρώντας κατά μέλη έπεται  . Συμπεραίνουμε
. Συμπεραίνουμε  (αλλιώς
(αλλιώς  που αντιβαίνει στην υπόθεση). Η
που αντιβαίνει στην υπόθεση). Η  τώρα γράφεται
τώρα γράφεται  , από όπου το ζητούμενο.
, από όπου το ζητούμενο.




 τότε
τότε  [1] και αντίστοιχα
[1] και αντίστοιχα  [2]
[2] εικόνες αντίστοιχα των
εικόνες αντίστοιχα των  τότε
τότε οι ευθείες
οι ευθείες  είναι διαφορετικές
είναι διαφορετικές συνευθειακά ,
συνευθειακά ,  συνευθειακά
συνευθειακά![\displaystyle{[3]\Rightarrow A, D, B} \displaystyle{[3]\Rightarrow A, D, B}](/forum/ext/geomar/texintegr/latexrender/pictures/d10987f72d6392373ec3eb8474c600f7.png) συνευθειακά και
συνευθειακά και 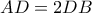
 συνευθειακά και
συνευθειακά και 
 με διατεμνουσα την
με διατεμνουσα την 
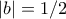 με
με  αφού το Ο ανάμεσα στα Α,Ε επεται
αφού το Ο ανάμεσα στα Α,Ε επεται  και από την [2] το ζητούμενο
Υ.Γ
και από την [2] το ζητούμενο
Υ.Γ σε γενική θέση δηλαδή να σχηματίζουν τρίγωνο. Α μετατρέψουμε τις σχέσεις [1],[2] σε διανυσματικές φαίνεται καθαρά γιατί τα
σε γενική θέση δηλαδή να σχηματίζουν τρίγωνο. Α μετατρέψουμε τις σχέσεις [1],[2] σε διανυσματικές φαίνεται καθαρά γιατί τα  βρίσκονται πάνω στις πλευρές και όχι στις προεκτάσεις τους
βρίσκονται πάνω στις πλευρές και όχι στις προεκτάσεις τουςΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες