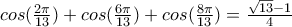

Νομίζω ότι όλες έχουν την ίδια λογική.Βασικά τα ριζικά με δυσκολεύουν διότι σε άλλες περιπτώσεις χρησιμοποιείς τον τύπο

και βγαίνει πιο εύκολα το ζητούμενο.
Συντονιστές: cretanman, Demetres, polysot, achilleas, socrates, silouan
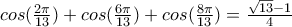


Μάλλον την έχουμε ξαναδεί, αλλά δε μπορώ να τη βρω.Rafaelcrete έγραψε:

 η παρένθεση γράφεται
η παρένθεση γράφεται
 ανάγεται στην
ανάγεται στην
 είναι
είναι και με τη βοήθεια του μετασχηματισμού
και με τη βοήθεια του μετασχηματισμού  βρίσκουμε
βρίσκουμε
εδώmatha έγραψε: Να αποδείξετε, ότι
εδώ,εδώ , εδώΓιώργος Απόκης έγραψε: Να δείξετε ότι
εδώchris_gatos έγραψε: Aντότε να υπολογίσετε την τιμή της παράστασης
εδώΦωτεινή έγραψε:Να αποδείξετε ότι
εδώerxmer έγραψε:Να αποδειχθεί οτι
εδώΦωτεινή έγραψε:Να αποδείξετε ότι
εδώchris_gatos έγραψε:Να υπολογίσετε την τιμή του αθροίσματος
εδώΦωτεινή έγραψε:Να αποδείξετε ότι
εδώΦωτεινή έγραψε:Να αποδείξετε ότι
Ελπίζω να μην χάνω κάποια απλούστερη προσέγγιση.Rafaelcrete έγραψε:
.


 ενώ στους τρεις τελευταίους την
ενώ στους τρεις τελευταίους την 
 (
( )
)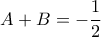 (απόδειξη παρακάτω), οπότε λόγω της (
(απόδειξη παρακάτω), οπότε λόγω της ( ) βρίσκουμε
) βρίσκουμε και επειδή
και επειδή  είναι
είναι 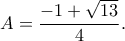
 φαίνεται και ως εξής:
φαίνεται και ως εξής:  και
και 





Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες