GI_A_ALG_4_13093
Ο ιδιοκτήτης ενός ταξιδιωτικού γραφείου εκτιμά ότι, όταν για μια συγκεκριμένη διαδρομή
διαθέτει τα εισιτήρια στην κανονική τιμή των

€ ανά εισιτήριο, τότε πουλά κατά μέσο όρο

μόνο εισιτήρια, ενώ το λεωφορείο έχει

θέσεις.
Θέλοντας να αυξήσει τη πελατεία του, κάνει την ακόλουθη προσφορά: Ο πρώτος επιβάτης
που θα αγοράσει εισιτήριο θα πληρώσει

€ και κάθε επόμενος επιβάτης θα πληρώνει

€ περισσότερο από τον προηγούμενο.
α) Να βρείτε το ποσό που θα πληρώσει ο δεύτερος, ο τρίτος και ο τέταρτος επιβάτης.
(Μονάδες

)
β) Αν, για κάθε

ο αριθμός αν εκφράζει το ποσό που θα πληρώσει ο ν-οστός
επιβάτης, να δείξετε ότι οι αριθμοί

είναι διαδοχικοί όροι αριθμητικής προόδου και να βρείτε τη διαφορά

αυτής της προόδου. (Μονάδες

)
γ) Αν το λεωφορείο γεμίσει, να βρείτε το ποσό που θα πληρώσει ο

ος επιβάτης.(Μονάδες

)
δ) Να βρείτε πόσα τουλάχιστον εισιτήρια θα πρέπει να πουληθούν ώστε η είσπραξη του
γραφείου με αυτή την προσφορά να ξεπερνά την είσπραξη που θα έκανε αν πουλούσε

εισιτήρια στην τιμή των

€ ανά εισιτήριο.
(Δίνεται ότι:

) (Μονάδες

)
Λύση.
α) Ο δεύτερος ο τρίτος και ο τέταρτος επιβάτης θα πληρώσουν αντίστοιχα,

€,

€ ,

€
β) Οι αριθμοί

είναι διαδοχικοί όροι αριθμητικής προόδου γιατί ο καθένας(μετά τον

) προκύπτει από τον προηγούμενο με πρόσθεση του ίδιου αριθμού

, που είναι και η διαφορά της προόδου.
γ) Ο

ος επιβάτης θα πληρώσει

€
δ) Για να συμβεί αυτό θα πρέπει:

, όπου

το άθροισμα των

πρώτων όρων της αριθμητικής προόδου.
![\displaystyle{\frac{{[2{a_1} + (n - 1)w]n}}{2} > 630 \Leftrightarrow 6n + \frac{1}{2}{n^2} - \frac{1}{2}n > 1260 \Leftrightarrow } \displaystyle{\frac{{[2{a_1} + (n - 1)w]n}}{2} > 630 \Leftrightarrow 6n + \frac{1}{2}{n^2} - \frac{1}{2}n > 1260 \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/76e020e4b13c64e3303c8c8352f970ee.png)
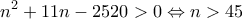
Θα πρέπει λοιπόν να πουληθούν τουλάχιστον

εισιτήρια.
ΣΧΟΛΙΟ: Το σχόλιο μου δεν είναι μαθηματικής φύσης, αλλά αφορά στη ευφυέστατη ιδέα του ιδιοκτήτη του ταξιδιωτικού γραφείου. Με το πανέξυπνο αυτό σχέδιο, ο

ος επιβάτης θα πληρώσει την κανονική τιμή, δηλαδή

€. Για να συμφέρει αυτή η ιδέα, θα πρέπει να πουληθούν τουλάχιστον άλλα

εισιτήρια. Η απορία μου είναι η εξής: Σ' ένα λεωφορείο που σε κανονική βάση πηγαίνει μισοάδειο, γιατί άραγε να βρεθούν

κορόιδα που να πληρώσουν το εισιτήριο με "καπέλο";


 καθίσματα περισσότερα από την προηγούμενη. Η
καθίσματα περισσότερα από την προηγούμενη. Η  σειρά έχει
σειρά έχει  καθίσματα και το πλήθος των καθισμάτων του σταδίου είναι
καθίσματα και το πλήθος των καθισμάτων του σταδίου είναι  .
. και
και  .
. και βρίσκουμε
και βρίσκουμε 


 οι μαθητές από το
οι μαθητές από το  ως το
ως το  ;
;  μέτρα και
μέτρα και  μέτρα.
μέτρα. )
) )
) η περίμετρος και
η περίμετρος και  το εμβαδόν του πατώματος.
το εμβαδόν του πατώματος. ,
, 
 ,
,  ή
ή  που απορρίπτεται.
που απορρίπτεται. μέτρα και
μέτρα και  με
με 
 για κάθε
για κάθε  όπου
όπου  η διακρίνουσα του τριωνύμου. (Μονάδες 10)
η διακρίνουσα του τριωνύμου. (Μονάδες 10) είναι οι ρίζες της εξίσωσης
είναι οι ρίζες της εξίσωσης  (1),
(1), i) να βρείτε το άθροισμα
i) να βρείτε το άθροισμα  και το γινόμενο
και το γινόμενο  των ριζών της (1) (Μονάδες 6)
των ριζών της (1) (Μονάδες 6) βαθμού που να έχει ρίζες
βαθμού που να έχει ρίζες  , όπου
, όπου  και
και 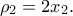 (Μονάδες 9)
(Μονάδες 9)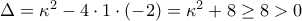 για κάθε
για κάθε  και
και 



 και
και  , όπου
, όπου 
 ℝ
ℝ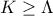 , για κάθε τιμή των
, για κάθε τιμή των  ; Να αιτιολογήσετε την απάντησή σας.
; Να αιτιολογήσετε την απάντησή σας. )
)


 , με παράμετρο
, με παράμετρο 
 .
. ώστε η εξίσωση να είναι
ώστε η εξίσωση να είναι  ου βαθμού. (Μονάδες
ου βαθμού. (Μονάδες  )
) ου βαθμού, να βρείτε τις τιμές του
ου βαθμού, να βρείτε τις τιμές του  είναι μη αρνητικό, για κάθε πραγματικό αριθμό x. (Μονάδες
είναι μη αρνητικό, για κάθε πραγματικό αριθμό x. (Μονάδες 
 και
και 

 η εξίσωση γράφεται:
η εξίσωση γράφεται: 
 η εξίσωση γράφεται:
η εξίσωση γράφεται: 
 το τριώνυμο γράφεται αντίστοιχα:
το τριώνυμο γράφεται αντίστοιχα:  και
και  , για κάθε
, για κάθε 

 . (Μονάδες
. (Μονάδες  το τριώνυμο έχει ρίζες πραγματικές και άνισες.
το τριώνυμο έχει ρίζες πραγματικές και άνισες. τότε:
τότε: συναρτήσει του
συναρτήσει του  των ριζών του. (Μονάδες
των ριζών του. (Μονάδες  (Μονάδες
(Μονάδες  )
)

 , που αληθεύει εκτός των ριζών του τριωνύμου. Οι ρίζες του είναι
, που αληθεύει εκτός των ριζών του τριωνύμου. Οι ρίζες του είναι  . Άρα:
. Άρα: 




 , η οποία έχει πεδίο ορισμού το
, η οποία έχει πεδίο ορισμού το 
 και
και  . (Mονάδες 9)
. (Mονάδες 9)  και
και  ,
,  . (Μονάδες 9)
. (Μονάδες 9)  όταν
όταν  . (Μονάδες 7)
. (Μονάδες 7) ο παρονομαστής είναι διάφορος του μηδενός για κάθε
ο παρονομαστής είναι διάφορος του μηδενός για κάθε  , οπότε μπορούμε να θεωρήσουμε μια συνάρτηση
, οπότε μπορούμε να θεωρήσουμε μια συνάρτηση  με πεδίο ορισμού το
με πεδίο ορισμού το 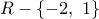 .
. , το
, το  έχει ρίζα
έχει ρίζα  , οπότε αρκεί
, οπότε αρκεί  και
και 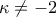 .
. , για να έχει πεδίο ορισμού το
, για να έχει πεδίο ορισμού το 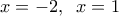 .
.
 που έχει μοναδικές ρίζες τα
που έχει μοναδικές ρίζες τα  είναι το
είναι το 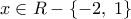
 και
και 
 , με
, με 
 ανήκουν στο πεδίο ορισμού της
ανήκουν στο πεδίο ορισμού της  δηλαδή
δηλαδή 
 , έχουμε
, έχουμε
![\displaystyle
\Leftrightarrow \left( {\alpha + 4} \right)\left( {\alpha + 1} \right) - \left( {\alpha + 1} \right)\left( {\alpha - 2} \right) > 0 \Leftrightarrow \left( {\alpha + 1} \right)\left[ {\left( {\alpha + 4} \right) - \left( {\alpha - 2} \right)} \right] > 0 \displaystyle
\Leftrightarrow \left( {\alpha + 4} \right)\left( {\alpha + 1} \right) - \left( {\alpha + 1} \right)\left( {\alpha - 2} \right) > 0 \Leftrightarrow \left( {\alpha + 1} \right)\left[ {\left( {\alpha + 4} \right) - \left( {\alpha - 2} \right)} \right] > 0](/forum/ext/geomar/texintegr/latexrender/pictures/d33d8d00f8d3edf701ba8a199869dc9c.png)
 , οπότε με βάση τους περιορισμούς είναι
, οπότε με βάση τους περιορισμούς είναι 
 , να δείξετε ότι:
, να δείξετε ότι:  , που ισχύει, εφόσον η παραπάνω ένωση διαστημάτων είναι υποσύνολο του
, που ισχύει, εφόσον η παραπάνω ένωση διαστημάτων είναι υποσύνολο του 
 που δίνονται ισχύει η ανίσωση.
που δίνονται ισχύει η ανίσωση.
 . (Μονάδες
. (Μονάδες  )
)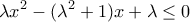 , για κάθε
, για κάθε  .
.
 και
και  . Αλλά είναι
. Αλλά είναι 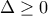 , για κάθε
, για κάθε  , δηλαδή
, δηλαδή  το τριώνυμο
το τριώνυμο , για κάθε
, για κάθε  ,
,  , για κάθε
, για κάθε  , τότε το τριώνυμο έχει δύο ρίζες πραγματικές και άνισες, οπότε δεν έχει σταθερό πρόσημο.
, τότε το τριώνυμο έχει δύο ρίζες πραγματικές και άνισες, οπότε δεν έχει σταθερό πρόσημο. με Δ=0, οπότε η εξίωση έχει διπλή ρίζα.
με Δ=0, οπότε η εξίωση έχει διπλή ρίζα. την οποία αν πάρουμε ίση με 0 έχουμε ότι αυτό πραγματοποιείται για λ=5 ή λ= - 1.
την οποία αν πάρουμε ίση με 0 έχουμε ότι αυτό πραγματοποιείται για λ=5 ή λ= - 1. >0
>0 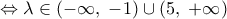
 για τις τιμές τις οποίες η διακρίνουσα της αρχικής εξίσωσης είναι αρνητική και επομένως δεν έχει πραγματικές ρίζες.
για τις τιμές τις οποίες η διακρίνουσα της αρχικής εξίσωσης είναι αρνητική και επομένως δεν έχει πραγματικές ρίζες.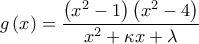 , η οποία έχει πεδίο ορισμού το
, η οποία έχει πεδίο ορισμού το 
 και
και  . (Mονάδες 9)
. (Mονάδες 9)  και
και  ,
,  όταν
όταν  . (Μονάδες 7)
. (Μονάδες 7)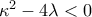 ο παρονομαστής είναι διάφορος του μηδενός για κάθε
ο παρονομαστής είναι διάφορος του μηδενός για κάθε  , οπότε μπορούμε να θεωρήσουμε μια συνάρτηση
, οπότε μπορούμε να θεωρήσουμε μια συνάρτηση  , το
, το  έχει ρίζα
έχει ρίζα  .
. , για να έχει πεδίο ορισμού το
, για να έχει πεδίο ορισμού το  πρέπει να είναι μηδέν ο παρονομαστής του μόνο όταν είναι
πρέπει να είναι μηδέν ο παρονομαστής του μόνο όταν είναι 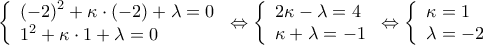
 που έχει μοναδικές ρίζες τα
που έχει μοναδικές ρίζες τα  , οπότε το πεδίο ορισμού της
, οπότε το πεδίο ορισμού της 
 και
και  ,
,  , με
, με 
 , οπότε
, οπότε
 , θα έπρεπε να το διατυπώσουν σαφέστερα:
, θα έπρεπε να το διατυπώσουν σαφέστερα:  για τις οποίες ισχύει η ανισότητα, κάτι που το βρίσκω αρκετά δύσκολο για μαθητές Α΄ Λυκείου.
για τις οποίες ισχύει η ανισότητα, κάτι που το βρίσκω αρκετά δύσκολο για μαθητές Α΄ Λυκείου. ανήκουν στο πεδίο ορισμού της
ανήκουν στο πεδίο ορισμού της 

 ή
ή  ή
ή 
 ή
ή 
 και
και  και συνδύασα τις περιπτώσεις να είναι ομόσημες.
και συνδύασα τις περιπτώσεις να είναι ομόσημες.  και
και  ,
,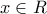
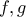 έχουν ένα μόνο κοινό
έχουν ένα μόνο κοινό . Να δείξετε ότι:
. Να δείξετε ότι: , τότε οι γραφικές παραστάσεις των συναρτήσεων
, τότε οι γραφικές παραστάσεις των συναρτήσεων  έχουν δύο κοινά σημεία.
έχουν δύο κοινά σημεία. , τότε οι γραφικές παραστάσεις των συναρτήσεων
, τότε οι γραφικές παραστάσεις των συναρτήσεων  , απ' όπου
, απ' όπου  . Άρα οι γραφικές παραστάσεις των δύο συναρτήσεων έχουν ένα μόνο κοινό σημεία, το
. Άρα οι γραφικές παραστάσεις των δύο συναρτήσεων έχουν ένα μόνο κοινό σημεία, το  .
. , θα προσδιορίσουμε και το πλήθος των σημείων τομής των γραφικών τους παραστάσεων.
, θα προσδιορίσουμε και το πλήθος των σημείων τομής των γραφικών τους παραστάσεων.
 , οπότε η εξίσωση έχει δύο ρίζες πραγματικές και άνισες. Άρα οι γραφικές παραστάσεις των συναρτήσεων
, οπότε η εξίσωση έχει δύο ρίζες πραγματικές και άνισες. Άρα οι γραφικές παραστάσεις των συναρτήσεων  έχουν δύο κοινά σημεία.
έχουν δύο κοινά σημεία. , τότε
, τότε  , οπότε η εξίσωση δεν έχει πραγματικές ρίζες. Άρα οι γραφικές παραστάσεις των συναρτήσεων
, οπότε η εξίσωση δεν έχει πραγματικές ρίζες. Άρα οι γραφικές παραστάσεις των συναρτήσεων  τετραγωνικά μίλια (τ.μ), στο τέλος της 2
τετραγωνικά μίλια (τ.μ), στο τέλος της 2 ης ημέρας καλύπτει
ης ημέρας καλύπτει  )
) τ.μ.;
τ.μ.;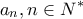 , όπου ο πρώτος όρος είναι
, όπου ο πρώτος όρος είναι  και ο λόγος
και ο λόγος  . Στο τέλος της
. Στο τέλος της  τ. μ.
τ. μ. ώστε
ώστε  .
. .
. , όπου ο πρώτος όρος είναι
, όπου ο πρώτος όρος είναι  , η διαφορά της προόδου
, η διαφορά της προόδου  και ο νιοστός όρος
και ο νιοστός όρος  . Έχουμε λοιπόν:
. Έχουμε λοιπόν:
 ημέρες από τη στιγμή που επενέβη ο κρατικός μηχανισμός, δηλαδή σε
ημέρες από τη στιγμή που επενέβη ο κρατικός μηχανισμός, δηλαδή σε  ημέρες από τη στιγμή του ατυχήματος, η θαλάσσια επιφάνεια που καλύπτεται από το πετρέλαιο θα έχει περιοριστεί στα
ημέρες από τη στιγμή του ατυχήματος, η θαλάσσια επιφάνεια που καλύπτεται από το πετρέλαιο θα έχει περιοριστεί στα  € ανά εισιτήριο, τότε πουλά κατά μέσο όρο
€ ανά εισιτήριο, τότε πουλά κατά μέσο όρο  μόνο εισιτήρια, ενώ το λεωφορείο έχει
μόνο εισιτήρια, ενώ το λεωφορείο έχει θέσεις.
θέσεις. € περισσότερο από τον προηγούμενο.
€ περισσότερο από τον προηγούμενο. ο αριθμός αν εκφράζει το ποσό που θα πληρώσει ο ν-οστός
ο αριθμός αν εκφράζει το ποσό που θα πληρώσει ο ν-οστός είναι διαδοχικοί όροι αριθμητικής προόδου και να βρείτε τη διαφορά
είναι διαδοχικοί όροι αριθμητικής προόδου και να βρείτε τη διαφορά  αυτής της προόδου. (Μονάδες
αυτής της προόδου. (Μονάδες  ) (Μονάδες
) (Μονάδες  €,
€,  €
€  ) προκύπτει από τον προηγούμενο με πρόσθεση του ίδιου αριθμού
) προκύπτει από τον προηγούμενο με πρόσθεση του ίδιου αριθμού  , που είναι και η διαφορά της προόδου.
, που είναι και η διαφορά της προόδου. €
€ , όπου
, όπου  το άθροισμα των
το άθροισμα των ![\displaystyle{\frac{{[2{a_1} + (n - 1)w]n}}{2} > 630 \Leftrightarrow 6n + \frac{1}{2}{n^2} - \frac{1}{2}n > 1260 \Leftrightarrow } \displaystyle{\frac{{[2{a_1} + (n - 1)w]n}}{2} > 630 \Leftrightarrow 6n + \frac{1}{2}{n^2} - \frac{1}{2}n > 1260 \Leftrightarrow }](/forum/ext/geomar/texintegr/latexrender/pictures/76e020e4b13c64e3303c8c8352f970ee.png)
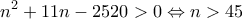
 εισιτήρια.
εισιτήρια. συναρτήσει
συναρτήσει και να βρείτε την τιμή του γινομένου
και να βρείτε την τιμή του γινομένου 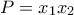 των ριζών.(Μονάδες
των ριζών.(Μονάδες  το παραπάνω τριώνυμο έχει ρίζες θετικές ή αρνητικές; Να αιτιολογήσετε την απάντησή σας. (Μονάδες
το παραπάνω τριώνυμο έχει ρίζες θετικές ή αρνητικές; Να αιτιολογήσετε την απάντησή σας. (Μονάδες  και
και  , είναι οι ρίζες του παραπάνω τριωνύμου, τότε να βρείτε το πρόσημο του γινομένου
, είναι οι ρίζες του παραπάνω τριωνύμου, τότε να βρείτε το πρόσημο του γινομένου  , όπου
, όπου  είναι αριθμοί τέτοιοι ώστε
είναι αριθμοί τέτοιοι ώστε  . (Μονάδες
. (Μονάδες  . Άρα το τριώνυμο έχει ρίζες πραγματικές για κάθε
. Άρα το τριώνυμο έχει ρίζες πραγματικές για κάθε 



 .
.
 και
και  με πεδίο ορισμού το
με πεδίο ορισμού το  .
. . (Μονάδες 6)
. (Μονάδες 6) τέμνει τους άξονες σε κάποιο από τα σημεία
τέμνει τους άξονες σε κάποιο από τα σημεία  και
και  . (Μονάδες 4)
. (Μονάδες 4) δεν έχουν κοινό σημείο πάνω σε κάποιον από τους άξονες. (Μονάδες 8)
δεν έχουν κοινό σημείο πάνω σε κάποιον από τους άξονες. (Μονάδες 8) της οποίας η γραφική παράσταση είναι ευθεία, διέρχεται από το
της οποίας η γραφική παράσταση είναι ευθεία, διέρχεται από το  και τέμνει τη γραφική παράσταση της
και τέμνει τη γραφική παράσταση της  . (Μονάδες 7)
. (Μονάδες 7) , δηλαδή στα σημεία
, δηλαδή στα σημεία 
 , οπότε η γραφική παράσταση της
, οπότε η γραφική παράσταση της  .
. και
και  άρα ούτε στον άξονα
άρα ούτε στον άξονα  τέμνονται.
τέμνονται.  .
. έχει γραφική παράσταση που είναι πλάγια ευθεία της μορφής
έχει γραφική παράσταση που είναι πλάγια ευθεία της μορφής  και διέρχεται από τα σημεία
και διέρχεται από τα σημεία 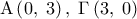 .
. 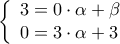 οπότε
οπότε  , άρα
, άρα 
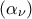 , όπου
, όπου  .
.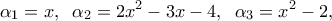 όπου
όπου 
 . (Μονάδες 10)
. (Μονάδες 10) . (Μονάδες 7)
. (Μονάδες 7)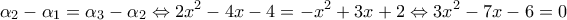 , όπου
, όπου  , άρα η ακέραιη ρίζα είναι
, άρα η ακέραιη ρίζα είναι 
 άρα
άρα  ,
, 
 γράφεται
γράφεται 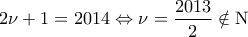 , άρα είναι αδύνατη.
, άρα είναι αδύνατη. που είναι επίσης αριθμητική πρόοδος με πρώτο όρο
που είναι επίσης αριθμητική πρόοδος με πρώτο όρο  και διαφορά
και διαφορά  , άρα
, άρα 
 , άρα
, άρα  .
.
 .
. 
 είναι τρία ενδεχόμενα ενός δειγματικού χώρου Ω ενός πειράματος τύχης, να διατυπώσετε λεκτικά τα παρακάτω ενδεχόμενα:
είναι τρία ενδεχόμενα ενός δειγματικού χώρου Ω ενός πειράματος τύχης, να διατυπώσετε λεκτικά τα παρακάτω ενδεχόμενα: ii)
ii)  iii)
iii)  iv)
iv)  (Μονάδες 12)
(Μονάδες 12) και
και  αυτού.
αυτού. με
με 
 με
με 
 με
με ![\displaystyle{N\left[ \left( A\bigcap B \right)\bigcap \Gamma \right]=1} \displaystyle{N\left[ \left( A\bigcap B \right)\bigcap \Gamma \right]=1}](/forum/ext/geomar/texintegr/latexrender/pictures/e0049f19e6d3bd13351ef8f6b6f86c9f.png)
 με
με 



![\displaystyle{P\left[ \left( A\bigcap B \right)\bigcap \Gamma \right]=\frac{N\left[ \left( A\bigcap B \right)\bigcap \Gamma \right]}{N\left( \Omega \right)}=\frac{1}{12}} \displaystyle{P\left[ \left( A\bigcap B \right)\bigcap \Gamma \right]=\frac{N\left[ \left( A\bigcap B \right)\bigcap \Gamma \right]}{N\left( \Omega \right)}=\frac{1}{12}}](/forum/ext/geomar/texintegr/latexrender/pictures/0ef6242f9deaadf00d72661fac13d4f9.png)
