 έχει τις κορυφές του
έχει τις κορυφές του  πάνω στις πλευρές
πάνω στις πλευρές  ορθογωνίου τριγώνου
ορθογωνίου τριγώνου  έτσι ώστε
έτσι ώστε  Να βρείτε συναρτήσει του
Να βρείτε συναρτήσει του  τις πλευρές του ορθογωνίου τριγώνου που έχει
τις πλευρές του ορθογωνίου τριγώνου που έχει το ελάχιστο εμβαδόν, καθώς και το εμβαδόν αυτό.
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 έχει τις κορυφές του
έχει τις κορυφές του  πάνω στις πλευρές
πάνω στις πλευρές  ορθογωνίου τριγώνου
ορθογωνίου τριγώνου  έτσι ώστε
έτσι ώστε  Να βρείτε συναρτήσει του
Να βρείτε συναρτήσει του  τις πλευρές του ορθογωνίου τριγώνου που έχει
τις πλευρές του ορθογωνίου τριγώνου που έχει Έστωgeorge visvikis έγραψε:min-area.png
Ισόπλευρο τρίγωνο πλευράςέχει τις κορυφές του
πάνω στις πλευρές
ορθογωνίου τριγώνου
έτσι ώστε
Να βρείτε συναρτήσει του
τις πλευρές του ορθογωνίου τριγώνου που έχει το ελάχιστο εμβαδόν, καθώς και το εμβαδόν αυτό.
 και ας είναι
και ας είναι  η ορθή προβολή του
η ορθή προβολή του  στην
στην  . Τότε
. Τότε  (ύψος ισοπλεύρου τριγώνου πλευράς
(ύψος ισοπλεύρου τριγώνου πλευράς  ).
).
 .
. επιτυγχάνεται όταν μεγιστοποιηθεί η συνάρτηση
επιτυγχάνεται όταν μεγιστοποιηθεί η συνάρτηση 



 .
. ρίζες ως προς
ρίζες ως προς  πρέπει
πρέπει  και συνεπώς η ελάχιστη τιμή του
και συνεπώς η ελάχιστη τιμή του 
 όταν
όταν  για την τιμή της διπλής ρίζας της εξίσωσης
για την τιμή της διπλής ρίζας της εξίσωσης  ,
, 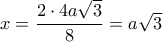 οπότε
οπότε 
 το μέσο της
το μέσο της  και από Πυθαγόρειο θεώρημα θα είναι
και από Πυθαγόρειο θεώρημα θα είναι  ,
,  και όλα τα ζητούμενα έχουν υπολογιστεί.
και όλα τα ζητούμενα έχουν υπολογιστεί. , έχουμε
, έχουμε  Αν
Αν  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  και θεωρήσουμε
και θεωρήσουμε  τότε επί της ουσίας είναι καθαρό ότι ζητάμε το ελάχιστο εμβαδόν του ορθογωνίου τριγώνου
τότε επί της ουσίας είναι καθαρό ότι ζητάμε το ελάχιστο εμβαδόν του ορθογωνίου τριγώνου  που προφανώς είναι μηδέν. Αλλά τότε έχουμε τη ταύτιση των σημείων
που προφανώς είναι μηδέν. Αλλά τότε έχουμε τη ταύτιση των σημείων  , οπότε
, οπότε  και έτσι στη περίπτωση αυτή άμεσα διαπιστώνουμε ότι
και έτσι στη περίπτωση αυτή άμεσα διαπιστώνουμε ότι 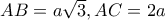 και βέβαια το ζητούμενο εμβαδόν είναι
και βέβαια το ζητούμενο εμβαδόν είναι 
 και σημείο
και σημείο  εντός αυτής. Θεωρούμε τυχούσα ευθεία
εντός αυτής. Θεωρούμε τυχούσα ευθεία  διερχόμενη από το
διερχόμενη από το  που τέμνει τις
που τέμνει τις  στα σημεία
στα σημεία  , αντίστοιχα. Βρείτε τη θέση της ευθείας
, αντίστοιχα. Βρείτε τη θέση της ευθείας  που το εμβαδόν του τριγώνου
που το εμβαδόν του τριγώνου  γίνεται ελάχιστο.
γίνεται ελάχιστο.Καλημέρα.S.E.Louridas έγραψε:Γεια χαρά στους Άριστους Γεωμέτρες αλλά και φίλους Γιώργο και Στάθη με όλες τις ευχές μου λόγω των ημερών.
Μία διαπραγμάτευση:
Ας θεωρήσουμε ότι κατά τη κίνηση της, έχουμε
Αν
το συμμετρικό του
ως προς το
και θεωρήσουμε
τότε επί της ουσίας είναι καθαρό ότι ζητάμε το ελάχιστο εμβαδόν του ορθογωνίου τριγώνου
που προφανώς είναι μηδέν. Αλλά τότε έχουμε τη ταύτιση των σημείων
, οπότε
και έτσι στη περίπτωση αυτή άμεσα διαπιστώνουμε ότι
και βέβαια το ζητούμενο εμβαδόν είναι

(*) Η μέθοδος αυτή επίλυσης λειτουργεί ακριβώς το ίδιο και στο ευρύτερο πρόβλημα:
Δίδεται γωνίακαι σημείο
εντός αυτής. Θεωρούμε τυχούσα ευθεία
διερχόμενη από το
που τέμνει τις
στα σημεία
, αντίστοιχα. Βρείτε τη θέση της ευθείας
που το εμβαδόν του τριγώνου
γίνεται ελάχιστο.
 . Αυτό επειδή τελικά η θέση για το ελάχιστο εμβαδόν του ορθογωνίου τριγώνου
. Αυτό επειδή τελικά η θέση για το ελάχιστο εμβαδόν του ορθογωνίου τριγώνου  καθορίζεται από το παραλληλόγραμμο (ορθογώνιο)
καθορίζεται από το παραλληλόγραμμο (ορθογώνιο)  .
. και σημείο
και σημείο  εντός αυτής. Θεωρούμε τυχούσα ευθεία
εντός αυτής. Θεωρούμε τυχούσα ευθεία  διερχόμενη από το
διερχόμενη από το  που τέμνει τις
που τέμνει τις  στα σημεία
στα σημεία  , αντίστοιχα. Βρείτε τη θέση της ευθείας
, αντίστοιχα. Βρείτε τη θέση της ευθείας  που το εμβαδόν του τριγώνου
που το εμβαδόν του τριγώνου  γίνεται ελάχιστο.
γίνεται ελάχιστο.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες