Εστω

Θεωρούμε
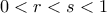
Να δειχθεί ότι

Συμπλήρωμα.
Αρκεί

Συντονιστές: achilleas, emouroukos, silouan

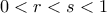


 , αρκεί, για
, αρκεί, για  , να δείξουμε ότι
, να δείξουμε ότι 
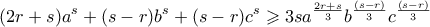
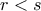 χρησιμοποιήθηκε για να είναι θετικοί οι συντελεστές στην ανισότητα ΑΜ-ΓΜ.]
χρησιμοποιήθηκε για να είναι θετικοί οι συντελεστές στην ανισότητα ΑΜ-ΓΜ.] . Είναι
. Είναι  και
και
 . Άρα η
. Άρα η  είναι αύξουσα.
είναι αύξουσα.Αν στηνDemetres έγραψε: Δεν ξέρω αν έχει όνομα αλλά αποδεικνύεται με την ανισότητα ΑΜ-ΓΜ με βάρη:
Πολλαπλασιάζοντας το αριστερό μέλος με το, αρκεί, για
, να δείξουμε ότι
Όμως από ΑΜ-ΓΜ έχουμε
Εφαρμόζοντας κυκλικά και προσθέτοντας έχουμε το ζητούμενο.
[Η συνθήκηχρησιμοποιήθηκε για να είναι θετικοί οι συντελεστές στην ανισότητα ΑΜ-ΓΜ.]


Η ανισότηταDemetres έγραψε: Δεν ξέρω αν έχει όνομα αλλά αποδεικνύεται με την ανισότητα ΑΜ-ΓΜ με βάρη:
Πολλαπλασιάζοντας το αριστερό μέλος με το, αρκεί, για
, να δείξουμε ότι
Όμως από ΑΜ-ΓΜ έχουμε
Εφαρμόζοντας κυκλικά και προσθέτοντας έχουμε το ζητούμενο.
[Η συνθήκηχρησιμοποιήθηκε για να είναι θετικοί οι συντελεστές στην ανισότητα ΑΜ-ΓΜ.]

 .
.

 .
.
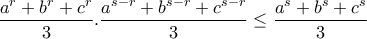

 )
) όταν
όταν 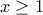 και την ανισότητα των δυνάμεων έχουμε ότι
και την ανισότητα των δυνάμεων έχουμε ότι  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 0 επισκέπτες