1. Να βρείτε όλες τις τριάδες των θετικών ακέραιων

που ικανοποιούν την εξίσωση

2. Αν
 είναι θετικοί πραγματικοί αριθμοί έτσι ώστε
είναι θετικοί πραγματικοί αριθμοί έτσι ώστε να δείξετε ότι
να δείξετε ότι 
3.Δίνεται το σταθερό κανονικό εννεάγωνο
 στο επίπεδο.
στο επίπεδο.  κορυφές του εννεάγωνο λέγονται «κανονική τριάδα» όταν σχηματίζουνε μία ισόπλευρο τρίγωνο. Σημειώνουμε κάθε κορυφή του εννεάγωνου με τους αριθμούς
κορυφές του εννεάγωνο λέγονται «κανονική τριάδα» όταν σχηματίζουνε μία ισόπλευρο τρίγωνο. Σημειώνουμε κάθε κορυφή του εννεάγωνου με τους αριθμούς  ή
ή  . Ένα εννεάγωνο λέγεται «τακτοποιημένο» όταν δεν έχει
. Ένα εννεάγωνο λέγεται «τακτοποιημένο» όταν δεν έχει  διαδοχικές κορυφές σημειωμένα με τον αριθμό μηδέν. Να βρείτε με πόσους τρόπους μπορούμε να σημειώνουμε το εννεάγωνο , έτσι ώστε οι αριθμοί των κάθε «κανονική τριάδα» έχουν άθροισμα
διαδοχικές κορυφές σημειωμένα με τον αριθμό μηδέν. Να βρείτε με πόσους τρόπους μπορούμε να σημειώνουμε το εννεάγωνο , έτσι ώστε οι αριθμοί των κάθε «κανονική τριάδα» έχουν άθροισμα  και το εννεάγωνο είναι «τακτοποιημένο».
και το εννεάγωνο είναι «τακτοποιημένο».4.Δίνεται το τρίγωνο
 (
( ) με περιεγραμμένο κύκλο
) με περιεγραμμένο κύκλο  και περίκεντρο
και περίκεντρο  . Οι εφαπτόμενες στο
. Οι εφαπτόμενες στο  από τα σημεία
από τα σημεία  και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  και το
και το  τέμνει την πλευρά
τέμνει την πλευρά  στο σημείο
στο σημείο  . Η ευθεία
. Η ευθεία  τέμνει τις ευθείες
τέμνει τις ευθείες  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα και η ευθεία
αντίστοιχα και η ευθεία 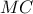 τέμνει την
τέμνει την  στο σημείο
στο σημείο  . Να δείξετε ότι το περιεγραμμένο κύκλο του τρίγωνου
. Να δείξετε ότι το περιεγραμμένο κύκλο του τρίγωνου  και ο κύκλος
και ο κύκλος  εφάπτονται.
εφάπτονται.
 , οπότε
, οπότε 

 .
. , που ισχύει, καθώς
, που ισχύει, καθώς  .
. έχουμε ότι
έχουμε ότι  .
. η εφαπτόμενη του κύκλου
η εφαπτόμενη του κύκλου  στο
στο  , και
, και  ένα σημείο της προς το ημιεπίπεδο που περιέχει το
ένα σημείο της προς το ημιεπίπεδο που περιέχει το  .
. .
. εφάπτονται στο
εφάπτονται στο 
 ή
ή  .
.
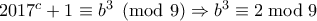 , που είναι άτοπο, καθώς
, που είναι άτοπο, καθώς  ή
ή  .
. .
. ή
ή 
 .
. , άτοπο.
, άτοπο. και δεύτερον πώς συμπέρανες ότι
και δεύτερον πώς συμπέρανες ότι  .Παίρνοντας
.Παίρνοντας  πράγμα το οποίο δεν αληθεύει την σχέση που έδωσες.Ανυπομονώ την απάντηση σου!
πράγμα το οποίο δεν αληθεύει την σχέση που έδωσες.Ανυπομονώ την απάντηση σου! , τότε είναι και
, τότε είναι και  Καταλήγουμε λοιπόν στο
Καταλήγουμε λοιπόν στο  .
. . Για να έχει κάθε τέτοια τριάδα άθροισμα δύο πρέπει να επιλέξουμε ακριβώς μια κορυφή από κάθε τριάδα στην οποία θα τοποθετήσουνε το
. Για να έχει κάθε τέτοια τριάδα άθροισμα δύο πρέπει να επιλέξουμε ακριβώς μια κορυφή από κάθε τριάδα στην οποία θα τοποθετήσουνε το  τρόποι να γίνει το πιο πάνω. Κάποιοι όμως δεν θα δώσουν τακτοποιημένο εννιάγωνο. Επειδή τοποπθετούμε ακριβώς
τρόποι να γίνει το πιο πάνω. Κάποιοι όμως δεν θα δώσουν τακτοποιημένο εννιάγωνο. Επειδή τοποπθετούμε ακριβώς 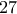 τρόπους, το πολύ
τρόπους, το πολύ  δίνουν μη τακτοποιημένα εννιάγωνα. Αυτοί που έχουν μηδενικά στις κορυφές
δίνουν μη τακτοποιημένα εννιάγωνα. Αυτοί που έχουν μηδενικά στις κορυφές  για
για  και τους δείκτες να είναι modulo
και τους δείκτες να είναι modulo  τρόπους ώστε κάθε κανονική τριάδα να έχει άθροισμα
τρόπους ώστε κάθε κανονική τριάδα να έχει άθροισμα