Nick1990 έγραψε:Ακόμα δύο θεματάκια απο παλιούς διαγωνισμούς "Αρχιμήδης", τα οποία μου άρεσαν ιδιαίτερα:
20.
Στο επίπεδο ορίζουμε μια διμελή πράξη *, τέτοια ώστε για κάθε δύο σημεία Χ,Υ του επιπέδου, το Χ*Υ να είναι το συμμετρικό σημείο του Χ ως προς το Υ. Ορίζουμε μια ακολουθία συνόλων

, ώστε για κάθε

να είναι

, με

το σύνολο των 3 απο τις 4 κορυφές ενός τετραγώνου στο επίπεδο. Είναι δυνατόν η τέταρτη κορυφή να ανήκει σε κάποιο από τα

???
Αν αυτό είναι το θέμα 4 του Αρχιμήδη 2003, το βιβλίο των θεμάτων που έχω λέει επίσης ότι "Δεν εξετάζονται οι πράξεις με σημεία που δεν ανήκουν στους άξονες x και y", το οποίο φυσικά δεν είναι απαραίτητο στη λύση του προβλήματος.
Έστω χωρίς βλάβη της γενικότητας ότι τα σημεία που έχουμε αρχικά είναι τα

. Αρχικά βλέπουμε ότι δουλεύουμε στους ακεραίους, αφού κάθε πράξη σημείων με ακέραιες συντεταγμένες έχει ως αποτέλεσμα σημείο με ακέραιες συντεταγμένες. Θα αποδείξουμε ότι δεν υπάρχει περίπτωση να προκύψει σημείο με συντεταγμένες της μορφής

. (τότε δε θα υπάρχει ούτε το (0,0) σε κάποιο σύνολο). Έστω

το πρώτο σύνολο που περιέχει ένα τέτοιο σημείο (το

δεν περιέχει κανένα τέτοιο σημείο). Τότε θα έχουμε ότι

και

, αν

, το οποίο σημαίνει ότι οι

είναι άρτιοι και είναι άτοπο αφού το σημείο

περιέχεται σε κάποιο σύνολο

.
 ,ώστε
,ώστε 
 .Τότε
.Τότε  .
. και άρα
και άρα  .
. ,δεν έχω λύση.Οπότε
,δεν έχω λύση.Οπότε  περιττός πρώτος κι επομένως
περιττός πρώτος κι επομένως  και λόγω της (2) θα είναι
και λόγω της (2) θα είναι  .
.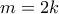 και η σχέση (1) γράφεται :
και η σχέση (1) γράφεται : .
.
 .
.
 λόγω της παραπάνω σχέσης θα είναι:
λόγω της παραπάνω σχέσης θα είναι: .
. ,έχουμε λύση
,έχουμε λύση

 ώστε ο
ώστε ο  να είναι πρώτος αριθμός.
να είναι πρώτος αριθμός.

![\displaystyle =\left[\left(a^2+b^2 \right)^{2}+b^4 \right]\left[\left(a^2-b^2 \right)^{2}+b^4 \right] \displaystyle =\left[\left(a^2+b^2 \right)^{2}+b^4 \right]\left[\left(a^2-b^2 \right)^{2}+b^4 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/38a465f0a64edbef8f67b5b69de3b28e.png)
 πρέπει κατα ανάγκην να είναι
πρέπει κατα ανάγκην να είναι  .
. θετικοί πραγματικοί αριθμοί, να δείξετε ότι
θετικοί πραγματικοί αριθμοί, να δείξετε ότι 

 δεν είναι ποτέ πρώτος.
δεν είναι ποτέ πρώτος. , δηλαδή
, δηλαδή  ή
ή  .
. για y=0 η αρχική δίνει
για y=0 η αρχική δίνει  , η οποία επαληθεύει την αρχική.
, η οποία επαληθεύει την αρχική. , άρα
, άρα  (που επαληθεύει την αρχική) ή
(που επαληθεύει την αρχική) ή  .
. . Για x=0 παίρνω
. Για x=0 παίρνω  , άρα
, άρα 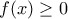 για κάθε
για κάθε  .
. ,
,  , άρα η f είναι περιττή και συνεπώς
, άρα η f είναι περιττή και συνεπώς  .
. η σχέση μας γίνεται
η σχέση μας γίνεται  με
με  ή
ή 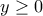 . Όμως
. Όμως  . Άρα
. Άρα  , η οποία είναι η συναρτησιακή Cauchy και οι λύσεις της είναι της μορφής
, η οποία είναι η συναρτησιακή Cauchy και οι λύσεις της είναι της μορφής 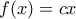 , όταν
, όταν  .
. και, αν
και, αν  να δειχθεί ότι ο
να δειχθεί ότι ο  είναι άρτιος τότε ο
είναι άρτιος τότε ο  είναι επίσης άρτιος μεγαλύτερος του
είναι επίσης άρτιος μεγαλύτερος του  και άρα ποτέ πρώτος.
και άρα ποτέ πρώτος. και έχουμε:
και έχουμε:
 και έτσι:
και έτσι:
 δεν είναι ποτέ πρώτος για
δεν είναι ποτέ πρώτος για  έχουμε:
έχουμε:  δηλαδή πρώτος)
δηλαδή πρώτος) τέτοια ώστε ο αριθμός
τέτοια ώστε ο αριθμός  να είναι ακέραιος.
να είναι ακέραιος. ένα υποσύνολο του
ένα υποσύνολο του  τέτοιο ώστε:
τέτοιο ώστε:  τέτοιες ώστε
τέτοιες ώστε  , για κάθε
, για κάθε  .
. υποσύνολο με την ιδιότητα αυτή, με
υποσύνολο με την ιδιότητα αυτή, με  .
.  είναι περιττος.
είναι περιττος.  , υπάρχουν δύο, έστω
, υπάρχουν δύο, έστω  , οπότε προφανώς
, οπότε προφανώς  . Κάνοντας το ίδιο με τα
. Κάνοντας το ίδιο με τα  προκείπτει
προκείπτει  .
. 


 όμως, και θα έχουμε:
όμως, και θα έχουμε:

 , και αυτός είναι και ο μέγιστος δυνατός πληθάριθμος ενός τέτοιου συνόλου διότι το σύνολο:
, και αυτός είναι και ο μέγιστος δυνατός πληθάριθμος ενός τέτοιου συνόλου διότι το σύνολο:
 προκείπτει
προκείπτει  , όπου
, όπου 
 και τότε:
και τότε: , και για
, και για 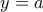 :
:

 θα πάρουμε:
θα πάρουμε:
 τέτοιες ώστε
τέτοιες ώστε  , όπου
, όπου  μη αρνητικοί ακέραιοι.
μη αρνητικοί ακέραιοι. πλευράς
πλευράς  . Να βρεθεί ο γεωμετρικός τόπος των σημείων
. Να βρεθεί ο γεωμετρικός τόπος των σημείων  του επιπέδου του έτσι ώστε
του επιπέδου του έτσι ώστε  .
. συναρτήσεις
συναρτήσεις  , για κάθε
, για κάθε 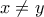 .
.![\displaystyle y^4+4=y^4+4\cdot1^4=\left(y^2+2 \right)^{2}-4y^{2}=\left[\left(y-1 \right)^{2}+1 \right]\left[\left(y+1 \right)^{2}+1 \right] \displaystyle y^4+4=y^4+4\cdot1^4=\left(y^2+2 \right)^{2}-4y^{2}=\left[\left(y-1 \right)^{2}+1 \right]\left[\left(y+1 \right)^{2}+1 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/5bf391698318a3b83ab25b00d452b952.png) . Άρα η αρχική είναι ισοδύναμη με την
. Άρα η αρχική είναι ισοδύναμη με την ![\displaystyle \left[\left(y-1 \right)^{2}+1 \right]\left[\left(y+1 \right)^{2}+1 \right]=p^x \displaystyle \left[\left(y-1 \right)^{2}+1 \right]\left[\left(y+1 \right)^{2}+1 \right]=p^x](/forum/ext/geomar/texintegr/latexrender/pictures/c8a16987479a807df0dd5ccee29f25a1.png) .
. , μια περίπτωση είναι να είναι
, μια περίπτωση είναι να είναι 
 .
. μιας και
μιας και  . Τότε όμως
. Τότε όμως ![\displaystyle p|\left(y-1 \right)^2+1 \wedge p|\left(y+1 \right)^2+1\Rightarrow p|\left[\left(y+1 \right)^2+1-\left(\left(y-1 \right)^2+1 \right) \right] \displaystyle p|\left(y-1 \right)^2+1 \wedge p|\left(y+1 \right)^2+1\Rightarrow p|\left[\left(y+1 \right)^2+1-\left(\left(y-1 \right)^2+1 \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/be45060584590a5f500779b96c1a979e.png)
 .
. τότε
τότε  . Άν λοιπόν
. Άν λοιπόν  τότε:
τότε:  .
. η εξίσωση είναι αδύνατη. Άρα εξετάζουμε την περίπτωση που
η εξίσωση είναι αδύνατη. Άρα εξετάζουμε την περίπτωση που  .
. δεν έχουμε λύση. Aν
δεν έχουμε λύση. Aν  . Άν
. Άν  η εξίσωση είναι αδύνατη.
η εξίσωση είναι αδύνατη.  , τότε ο
, τότε ο  τότε όμως
τότε όμως  η οποία είναι αδύνατη.
η οποία είναι αδύνατη. , τότε όμως θα είναι
, τότε όμως θα είναι  .
. .
. πραγματικοί αριθμοί τέτοιοι ώστε η εξίσωση
πραγματικοί αριθμοί τέτοιοι ώστε η εξίσωση  έχει πραγματικές ρίζες μεγαλύτερες του
έχει πραγματικές ρίζες μεγαλύτερες του  έχει μία τουλάχιστον πραγματική ρίζα.
έχει μία τουλάχιστον πραγματική ρίζα. η αρχική δίνει
η αρχική δίνει  .
. 
 παίρνουμε
παίρνουμε  η οποία καταλήγει στην
η οποία καταλήγει στην  .
. 
 ≠
≠ είναι σταθερή, άτοπο. Άρα
είναι σταθερή, άτοπο. Άρα  και από την
και από την  : περιττή.
: περιττή. δίνει
δίνει  .
. 
 , η
, η  .
. 
 .
. .
. με
με  :περιττό.
:περιττό. δίνει μετά από πράξεις
δίνει μετά από πράξεις  που φανερά έχει μοναδική λύση το
που φανερά έχει μοναδική λύση το 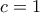 . Άρα
. Άρα  , ώστε για κάθε
, ώστε για κάθε  να είναι
να είναι  , με
, με  το σύνολο των 3 απο τις 4 κορυφές ενός τετραγώνου στο επίπεδο. Είναι δυνατόν η τέταρτη κορυφή να ανήκει σε κάποιο από τα
το σύνολο των 3 απο τις 4 κορυφές ενός τετραγώνου στο επίπεδο. Είναι δυνατόν η τέταρτη κορυφή να ανήκει σε κάποιο από τα  ???
??? , με
, με  , να ισχύει
, να ισχύει  . Να βρεθεί η ελάχιστη δυνατή τιμή του μεγαλύτερου απο τους 2011 θετικούς ακεραίους του συνόλου
. Να βρεθεί η ελάχιστη δυνατή τιμή του μεγαλύτερου απο τους 2011 θετικούς ακεραίους του συνόλου  . Αρχικά βλέπουμε ότι δουλεύουμε στους ακεραίους, αφού κάθε πράξη σημείων με ακέραιες συντεταγμένες έχει ως αποτέλεσμα σημείο με ακέραιες συντεταγμένες. Θα αποδείξουμε ότι δεν υπάρχει περίπτωση να προκύψει σημείο με συντεταγμένες της μορφής
. Αρχικά βλέπουμε ότι δουλεύουμε στους ακεραίους, αφού κάθε πράξη σημείων με ακέραιες συντεταγμένες έχει ως αποτέλεσμα σημείο με ακέραιες συντεταγμένες. Θα αποδείξουμε ότι δεν υπάρχει περίπτωση να προκύψει σημείο με συντεταγμένες της μορφής  . (τότε δε θα υπάρχει ούτε το (0,0) σε κάποιο σύνολο). Έστω
. (τότε δε θα υπάρχει ούτε το (0,0) σε κάποιο σύνολο). Έστω  το πρώτο σύνολο που περιέχει ένα τέτοιο σημείο (το
το πρώτο σύνολο που περιέχει ένα τέτοιο σημείο (το  δεν περιέχει κανένα τέτοιο σημείο). Τότε θα έχουμε ότι
δεν περιέχει κανένα τέτοιο σημείο). Τότε θα έχουμε ότι  και
και  , αν
, αν  , το οποίο σημαίνει ότι οι
, το οποίο σημαίνει ότι οι  είναι άρτιοι και είναι άτοπο αφού το σημείο
είναι άρτιοι και είναι άτοπο αφού το σημείο  περιέχεται σε κάποιο σύνολο
περιέχεται σε κάποιο σύνολο  .
. τέτοιες ώστε
τέτοιες ώστε  και
και 
 ένας πραγματικός αριθμός τέτοιος ώστε
ένας πραγματικός αριθμός τέτοιος ώστε  , για κάθε μη αρνητικό ακέραιο
, για κάθε μη αρνητικό ακέραιο  .
. πραγματικοί αριθμοί, να δείξετε ότι
πραγματικοί αριθμοί, να δείξετε ότι  .
.