 η εξίσωση
η εξίσωση  έχει τέσσερις πραγματικές ρίζες.
έχει τέσσερις πραγματικές ρίζες.Επιστροφή στην ειδική αναζήτηση
 η εξίσωση
η εξίσωση  έχει τέσσερις πραγματικές ρίζες.
έχει τέσσερις πραγματικές ρίζες. ένα πολυώνυμο
ένα πολυώνυμο  ου βαθμού με
ου βαθμού με  .
.
 .
.
 .
.

 είναι κορυφές ισοσκελούς τριγώνου στο μιγαδικό επίπεδο.
είναι κορυφές ισοσκελούς τριγώνου στο μιγαδικό επίπεδο. .
. ισχύει για κάθε
ισχύει για κάθε ![x \in [1,2] x \in [1,2]](/forum/ext/geomar/texintegr/latexrender/pictures/5e45ec4bc7e60fb589a8593c3007ea20.png)

 το ορθόκεντρο ενός τριγώνου
το ορθόκεντρο ενός τριγώνου  . Αν
. Αν  είναι το μέσο της πλευράς
είναι το μέσο της πλευράς 
 και είναι κάθετη στην
και είναι κάθετη στην  , τέμνει τις πλευρές του τριγώνου
, τέμνει τις πλευρές του τριγώνου 
 αντίστοιχα τότε να αποδείξετε ότι
αντίστοιχα τότε να αποδείξετε ότι 

 .
. ένα σημείο στο εσωτερικό ενός ισοπλεύρου τριγώνου
ένα σημείο στο εσωτερικό ενός ισοπλεύρου τριγώνου 
 .
. 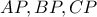 τέμνουν αντίστοιχα τις πλευρές
τέμνουν αντίστοιχα τις πλευρές  στα σημεία
στα σημεία 

 . Αν ισχύει
. Αν ισχύει  να υπολογίσετε τον
να υπολογίσετε τον  .
.