καλημέρα σε όλους
Τα θέματα ήταν πολύ ωραία ,χωρίς εκπλήξεις και οι μαθητές μπορούν άνετα να φθάσουν σε ένα καλό βαθμό.
Η αναζήτηση βρήκε 1247 εγγραφές
Επιστροφή στην ειδική αναζήτηση
- Τετ Ιουν 17, 2020 11:46 am
- Δ. Συζήτηση: Πανελλήνιες Εξετάσεις
- Θέμα: Σχόλια στα Μαθηματικά προσανατολισμού 2020
- Απαντήσεις: 75
- Προβολές: 20446
- Σάβ Απρ 01, 2017 8:39 pm
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Β'
- Θέμα: Ισεμβαδικά
- Απαντήσεις: 3
- Προβολές: 645
Re: Ισεμβαδικά
Είναι το δεύτερο με γωνίες 45 μοίρες.
- Σάβ Απρ 01, 2017 2:55 pm
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Β'
- Θέμα: Ισεμβαδικά
- Απαντήσεις: 3
- Προβολές: 645
Ισεμβαδικά
Μεσα σε ένα κύκλο γράφουμε το γράμμα Μ κεφαλαίο με τις 3 γωνίες του γράμματος Μ να είναι 45 μοιρών .
Δείξτε ότι η τεθλασμένη γραμμή του Μ , χωρίζει τον κύκλο σε δυο ισεμβαδικά μέρη .
φιλικά
dennys και καλο μήνα
Δείξτε ότι η τεθλασμένη γραμμή του Μ , χωρίζει τον κύκλο σε δυο ισεμβαδικά μέρη .
φιλικά
dennys και καλο μήνα
- Τετ Απρ 27, 2016 8:04 am
- Δ. Συζήτηση: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
- Θέμα: Ανισότητα
- Απαντήσεις: 4
- Προβολές: 1118
Re: Ανισότητα
Θάνο καλημέρα
Ευχαριστώ πολύ για την παρέμβασή σου .Προφανώς και είναι αυτό που είπες ,
αλλά θα ήθελα μια προσέγγιση συμφωνα με την υπόδειξη .
Με την ευκαιρία σου εύχομαι Καλό Πάσχα.
Διονυσης
Ευχαριστώ πολύ για την παρέμβασή σου .Προφανώς και είναι αυτό που είπες ,
αλλά θα ήθελα μια προσέγγιση συμφωνα με την υπόδειξη .
Με την ευκαιρία σου εύχομαι Καλό Πάσχα.
Διονυσης
- Τρί Απρ 26, 2016 11:41 pm
- Δ. Συζήτηση: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
- Θέμα: Ανισότητα
- Απαντήσεις: 4
- Προβολές: 1118
Ανισότητα
Να αποδειχθεί για την συνάρτηση
να αποδείξετε ότι
θέτοντας όπου , και θέτοντας συνάρτηση.
, και θέτοντας συνάρτηση.
φιλικά

να αποδείξετε ότι

θέτοντας όπου
 , και θέτοντας συνάρτηση.
, και θέτοντας συνάρτηση.φιλικά
- Δευ Απρ 18, 2016 1:38 pm
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Α'
- Θέμα: παραλληλογραμμα
- Απαντήσεις: 5
- Προβολές: 777
Re: παραλληλογραμμα
Κα λημερα κ. Μιχάλη
To Η είναι είναι η κάθετος απο το Α στην διαγώνιο ΒΔ.
To Η είναι είναι η κάθετος απο το Α στην διαγώνιο ΒΔ.
- Δευ Απρ 18, 2016 12:49 pm
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Α'
- Θέμα: παραλληλογραμμα
- Απαντήσεις: 5
- Προβολές: 777
παραλληλογραμμα
Δίνεται ορθ.παρ/μο ΑΒΓΔ και φέρουμε ΑΗ κάθετη στην ΒΔ, ΑΘ ,Θ μέσο ΔΓ, και γωνία ΑΟΒ=130..Δείξτε ότι ΑΔ=ΔΘ
ΦΙΛΙΚΆ
ΦΙΛΙΚΆ
- Πέμ Απρ 07, 2016 11:53 am
- Δ. Συζήτηση: ΑΣΚΗΣΕΙΣ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ Γ'
- Θέμα: Υπολογισμοί ολοκληρωμάτων
- Απαντήσεις: 2
- Προβολές: 856
Υπολογισμοί ολοκληρωμάτων
Βρείτε τα : α)$\int_{0}^{1}\cfrac{xe^x}{(e^x+1)^3}dx$ kai $\int_{0}^{1}\cfrac{x^2}{(x+1)^4}dx$ b)Aν $I_n=\int_{0}^{\pi/2}(sin^{n}x)dx$,να δείξετε ότι :1) $I_n I_{n-1}=\cfrac{\pi}{2n}$ 2)$I_n<I_{n-1}$ 3)$\lim_{n\to +\infty}I_n$
- Κυρ Απρ 03, 2016 12:18 pm
- Δ. Συζήτηση: ΑΣΚΗΣΕΙΣ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ Γ'
- Θέμα: Για τους μαθητές της Γ Λυκείου
- Απαντήσεις: 103
- Προβολές: 15488
Re: Για τους μαθητές της Γ Λυκείου
Ικανοποιούνται οι προϋποθέσει L'Hospital:$lim_{h\rightarrow 1}\frac{f(\frac{x}{h})-f(x)}{h-1}=lim_{h\rightarrow 1}\frac{f'(\frac{x}{h})(-\frac{x}{h^{2}}-0}){1}=-xf'(x) Άρα -xf'(x)=\frac{1}{x}+x-2\Leftrightarrow f'(x)=-\frac{1}{x^{2}}-1+\frac{2}{x} Επομένως f(x)=2lnx-x+\frac{1}{x}+c Για x=1 \rightar...
- Σάβ Μαρ 26, 2016 8:06 pm
- Δ. Συζήτηση: ΘΕΜΑΤΑ ΜΕ ΑΠΑΙΤΗΣΕΙΣ Γ'
- Θέμα: Μια κατασκευή...
- Απαντήσεις: 2
- Προβολές: 893
Re: Μια κατασκευή...
To Δ μάλλον είναι 

- Σάβ Μαρ 26, 2016 8:03 pm
- Δ. Συζήτηση: ΑΣΚΗΣΕΙΣ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ Γ'
- Θέμα: Για τους μαθητές της Γ Λυκείου
- Απαντήσεις: 103
- Προβολές: 15488
Re: Για τους μαθητές της Γ Λυκείου
ΑΣΚΗΣΗ 9 1) Το όριο γίνεται $\lim_{h\to 0}\cfrac{f(x+h)-f(x)+(h-1)f(x)}{sinh}= \lim_{h\to 0}(\cfrac{h}{sinh})(\cfrac{f(x+h)-f(x)}{h}+f(x))$ $(f'(x)+f(x))=(2x-3)e^{x}+e^{-x}\Rightarrow e^{x}(f'(x)+f(x))=(2x-3)e^{x}+1$, σχέση (1) 2)απο το (1) $(e^{x}f(x))'=[(2x-3)\cfrac{e^{2x}}{2}-\cfrac{e^{2x}}{2}+2+...
- Σάβ Μαρ 26, 2016 9:17 am
- Δ. Συζήτηση: ΑΣΚΗΣΕΙΣ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ Γ'
- Θέμα: βρείτε την f
- Απαντήσεις: 1
- Προβολές: 612
βρείτε την f
Δίνεται για την συνάρτηση 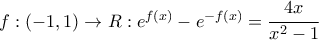
Βρείτε την
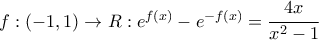
Βρείτε την
- Σάβ Μαρ 26, 2016 9:14 am
- Δ. Συζήτηση: Γενικά Μηνύματα
- Θέμα: XΡONIA ΠΟΛΛΑ
- Απαντήσεις: 29
- Προβολές: 2277
Re: XΡONIA ΠΟΛΛΑ
Xρόνια πολλά σε όλους τους συνάδελφους που γιορτάζουν .
Βουτσας Διονυσης
Βουτσας Διονυσης
- Κυρ Μαρ 20, 2016 11:21 pm
- Δ. Συζήτηση: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
- Θέμα: βρειτε την
- Απαντήσεις: 4
- Προβολές: 856
βρειτε την
Bρείτε την παραγωγίσιμη συνάρτηση  ,άν ισχύει :
,άν ισχύει : 
 ,άν ισχύει :
,άν ισχύει : 
- Τρί Μαρ 15, 2016 11:57 pm
- Δ. Συζήτηση: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ'
- Θέμα: βρείτε την f
- Απαντήσεις: 3
- Προβολές: 1411
βρείτε την f
3. Αν για την συνάρτηση ισχύει : ![f:[0,1]\rightarrow R,f(0)=0,f(1)=1,|f(x)-f(y)|\leq |x-y|,x,y\in[0,1] f:[0,1]\rightarrow R,f(0)=0,f(1)=1,|f(x)-f(y)|\leq |x-y|,x,y\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/23699500ab5e1addb6499a94ed2ff3c5.png) , . Βρείτε την f
, . Βρείτε την f
![f:[0,1]\rightarrow R,f(0)=0,f(1)=1,|f(x)-f(y)|\leq |x-y|,x,y\in[0,1] f:[0,1]\rightarrow R,f(0)=0,f(1)=1,|f(x)-f(y)|\leq |x-y|,x,y\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/23699500ab5e1addb6499a94ed2ff3c5.png) , . Βρείτε την f
, . Βρείτε την f- Σάβ Ιαν 23, 2016 9:18 pm
- Δ. Συζήτηση: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ'
- Θέμα: ΣΥΛΛΟΓΗ ΑΣΚΗΣΕΩΝ Γ'ΛΥΚΕΙΟΥ (ΝΕΑ ΥΛΗ)
- Απαντήσεις: 245
- Προβολές: 47197
Re: ΣΥΛΛΟΓΗ ΑΣΚΗΣΕΩΝ Γ'ΛΥΚΕΙΟΥ (ΝΕΑ ΥΛΗ)
ΑΣΚΗΣΗ 61 (Από βιβλίο του Χρήστου Πατήλα) Δίνεται η δύο φορές παραγωγίσιμη στο $R$ συνάρτηση $f: R \rightarrow R$ με τις ιδιότητες : $sin^{2}x+f'(tanx)=1$ , για κάθε $x \in (- \frac{\pi}{2} , \frac{\pi}{2})$ και $f(0)=0$. Α) Να δείξετε ότι η $f$ είναι γνησίως αύξουσα στο $R$. Β) Να βρείτε τις οριζό...
- Πέμ Ιαν 21, 2016 11:56 pm
- Δ. Συζήτηση: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ'
- Θέμα: ΣΥΛΛΟΓΗ ΑΣΚΗΣΕΩΝ Γ'ΛΥΚΕΙΟΥ (ΝΕΑ ΥΛΗ)
- Απαντήσεις: 245
- Προβολές: 47197
Re: ΣΥΛΛΟΓΗ ΑΣΚΗΣΕΩΝ Γ'ΛΥΚΕΙΟΥ (ΝΕΑ ΥΛΗ)
Οκ Βασίλη πάντα μάχιμος είσαι φίλε .
Τωρα συμφωνώ και σίγουρα ισχύει είναι απλή η απόδειξη.
Επίσης ή λύση που δίνεις στο γ) τώρα είναι αυτη που υπάρχει στο βιβλίο του δημιουργού
στην νεα έκδοση.
φιλικά
Τωρα συμφωνώ και σίγουρα ισχύει είναι απλή η απόδειξη.
Επίσης ή λύση που δίνεις στο γ) τώρα είναι αυτη που υπάρχει στο βιβλίο του δημιουργού
στην νεα έκδοση.
φιλικά
- Πέμ Ιαν 21, 2016 4:05 pm
- Δ. Συζήτηση: ΜΑΘΗΜΑΤΙΚΑ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΥ Γ'
- Θέμα: ΣΥΛΛΟΓΗ ΑΣΚΗΣΕΩΝ Γ'ΛΥΚΕΙΟΥ (ΝΕΑ ΥΛΗ)
- Απαντήσεις: 245
- Προβολές: 47197
Re: ΣΥΛΛΟΓΗ ΑΣΚΗΣΕΩΝ Γ'ΛΥΚΕΙΟΥ (ΝΕΑ ΥΛΗ)
Bασίλη είσαι σίγουρος για την τελευταία σχέση που ζητάς.
Για να ισχύει πρέπει η εκθετική να τέμνει την διχοτόμο. Εκτός και αν υπάρχει κάτι
που δεν το βλέπω .
πάντα φιλικά
Για να ισχύει πρέπει η εκθετική να τέμνει την διχοτόμο. Εκτός και αν υπάρχει κάτι
που δεν το βλέπω .
πάντα φιλικά
- Πέμ Ιαν 21, 2016 2:10 pm
- Δ. Συζήτηση: ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β'
- Θέμα: Άσκηση διαγωνίσματος
- Απαντήσεις: 7
- Προβολές: 1130
Re: Άσκηση διαγωνίσματος
Σωστό ειναι το β)
- Πέμ Ιαν 21, 2016 1:26 pm
- Δ. Συζήτηση: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
- Θέμα: Απορία σε παράγωγο
- Απαντήσεις: 6
- Προβολές: 1307
Re: Απορία σε παράγωγο
Αλέκο καλημέρα
Εχεις μια δυσπιστία χωρίς αιτία .Σου απάντησε ο G-Bas , τί άλλο πρέπει να σου πει κάποιος.
Οι τύποι των κανόνων ισχύουν και σε σημείο χο .Το βιβλίο την λύνει με ορισμό ,αλλά αυτό
δεν σημαίνει ότι δεν γίνεται και έτσι .
φιλικά
Εχεις μια δυσπιστία χωρίς αιτία .Σου απάντησε ο G-Bas , τί άλλο πρέπει να σου πει κάποιος.
Οι τύποι των κανόνων ισχύουν και σε σημείο χο .Το βιβλίο την λύνει με ορισμό ,αλλά αυτό
δεν σημαίνει ότι δεν γίνεται και έτσι .
φιλικά
