Η αναζήτηση βρήκε 3618 εγγραφές
Επιστροφή στην ειδική αναζήτηση
- Τρί Ιαν 13, 2026 7:18 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Ισεμβαδικά
- Απαντήσεις: 8
- Προβολές: 338
Re: Ισεμβαδικά
Στο ορθογώνιο τρίγωνο $ABC$ , η $CD$ είναι διχοτόμος και $AM$ διάμεσος . Ο κύκλος $(C , D , M )$ τέμνει την υποτείνουσα $BC$ στο σημείο $S$ . Δείξτε ότι : $(CDM)=(SDB)$ . shape.png Υ.Γ. Αν $T$ το σημείο τομής του κύκλου με την $AC$, τότε το $(ADT)$ είναι επίσης ισεμβαδικό με τα $X,Y$.
- Κυρ Δεκ 28, 2025 12:54 pm
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Β'
- Θέμα: Επίλυση τριγώνου
- Απαντήσεις: 2
- Προβολές: 156
- Σάβ Νοέμ 29, 2025 9:11 pm
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Προκαθορισμένο εμβαδόν
- Απαντήσεις: 5
- Προβολές: 214
- Κυρ Νοέμ 16, 2025 9:10 am
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Α'
- Θέμα: Εγγράψιμο
- Απαντήσεις: 20
- Προβολές: 1292
- Τετ Νοέμ 12, 2025 10:25 pm
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Α'
- Θέμα: Εγγράψιμο
- Απαντήσεις: 20
- Προβολές: 1292
- Τετ Νοέμ 12, 2025 7:07 pm
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Α'
- Θέμα: Εγγράψιμο
- Απαντήσεις: 20
- Προβολές: 1292
Re: Εγγράψιμο
Δίδεται ισοσκελές τρίγωνο $ABC\,\,\left( {b = c} \right)$ . Ας είναι $Z$ το μέσο της διαμέσου $AM$ και $K$ η προβολή του $M$ στην $BZ$. Δείξετε ότι το τετράπλευρο $AKMC$ είναι εγγράψιμο σε κύκλο . Δεκτές όλες οι λύσεις ( Γυμνασίου ή Λυκείου , με στοιχειώδη ή όχι εργαλεία) Παρόμοια με του Γιώργου. s...
- Τρί Νοέμ 11, 2025 9:32 pm
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Juniors)
- Θέμα: Η διχοτόμος
- Απαντήσεις: 4
- Προβολές: 256
- Πέμ Οκτ 30, 2025 4:08 pm
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Α'
- Θέμα: Κρυμμένη καθετότητα
- Απαντήσεις: 4
- Προβολές: 264
Re: Κρυμμένη καθετότητα
Έστω , $\vartriangle ABC$ εγγεγραμμένο σε κύκλο $O$. Οι εφαπτόμενες του κύκλου στα $B\,\,\kappa \alpha \iota \,\,\,C$ τέμνονται στο σημείο $P$. Από το $P$ φέρνουμε $PE\,\,,\,\,PZ$ κάθετες στις ευθείες $AB\,\,,\,\,AC$ αντίστοιχα . Να δειχθεί ότι η διάμεσος $AM$ του $\vartriangle ABC$ , είναι κάθετη ...
- Τετ Οκτ 29, 2025 7:28 am
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Β'
- Θέμα: Η γωνία A=60°
- Απαντήσεις: 3
- Προβολές: 200
Re: Η γωνία A=60°
Σε $\vartriangle ABC$ με $b > c$ η γωνία του $A = 60^\circ $ . . Η εσωτερική διχοτόμος $AD$ τέμνει τα ύψη $BE\,\,,CZ$ στα σημεία $K\,\,,\,\,L$ αντίστοιχα . Ας είναι $H$ το ορθόκεντρο του $\vartriangle ABC$. Δείξετε ότι το $\vartriangle HKL$ είναι ισόπλευρο και να υπολογιστεί η πλευρά του ,$KL$ ως έ...
- Δευ Οκτ 27, 2025 1:19 pm
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Άδικη διάμεσος
- Απαντήσεις: 6
- Προβολές: 309
- Δευ Οκτ 27, 2025 10:25 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Άδικη διάμεσος
- Απαντήσεις: 6
- Προβολές: 309
Re: Άδικη διάμεσος
Στις προεκτάσεις των πλευρών $BA , BC$ του - πλευράς $5$ - ισοπλεύρου τριγώνου $ABC$ , θεωρούμε σημεία $D , E$ αντίστοιχα , τέτοια ώστε : $AD=3 , CE=7$ . Αν $M$ το μέσο της $DE$ και η $BM$ τέμνει την $AC$ στο σημείο $S$ , υπολογίστε το τμήμα $AS$ . Screenshot_1.png $$Θέτω $T \equiv BM \cap CD$ και ...
- Πέμ Οκτ 02, 2025 7:20 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Διπλοκάθετες
- Απαντήσεις: 19
- Προβολές: 910
Re: Διπλοκάθετες
Σε ορθογώνιο τρίγωνο $ABC(\widehat A=90^\circ),$ είναι $M, N$ τα μέσα των $BC, AC$ αντίστοιχα και $D$ το μέσο του $AN.$ Αν $DM\bot BC,$ να δείξετε ότι $AM\bot BN.$ shape.png Θέτω $AD = k$ και από ομοιότητα, Πυθαγόρεια και το βαρύκεντρο $G$ καταλήγω σε αντίστροφο Πυθαγορείου στο $ \triangle NGM$, όπ...
- Τετ Οκτ 01, 2025 8:15 pm
- Δ. Συζήτηση: ΑΛΓΕΒΡΑ Β'
- Θέμα: Η ωραία διχοτόμος
- Απαντήσεις: 8
- Προβολές: 447
- Παρ Σεπ 26, 2025 6:34 am
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Β'
- Θέμα: Άνισα σε ισοσκελές
- Απαντήσεις: 3
- Προβολές: 316
- Τετ Σεπ 24, 2025 8:27 pm
- Δ. Συζήτηση: Γενικά - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Άλγεβρα ή Γεωμετρία ;
- Απαντήσεις: 3
- Προβολές: 262
- Δευ Σεπ 22, 2025 1:17 pm
- Δ. Συζήτηση: Γενικά - Επίπεδο Θαλή/Ευκλείδη (Juniors)
- Θέμα: Ειδικών διαστάσεων
- Απαντήσεις: 4
- Προβολές: 308
- Πέμ Σεπ 18, 2025 7:11 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Ανορθόδοξη ορθή
- Απαντήσεις: 5
- Προβολές: 718
- Πέμ Σεπ 11, 2025 5:59 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Juniors)
- Θέμα: Τραπεζιακές συναλλαγές
- Απαντήσεις: 1
- Προβολές: 482
- Κυρ Σεπ 07, 2025 11:44 am
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Β'
- Θέμα: Διακτινισμός
- Απαντήσεις: 7
- Προβολές: 700
- Παρ Σεπ 05, 2025 7:16 am
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Β'
- Θέμα: Κάντε την διαφορά
- Απαντήσεις: 5
- Προβολές: 747

 , με :
, με :  , η
, η  είναι διχοτόμος .
είναι διχοτόμος .  . Υπολογίστε την περίμετρο και το εμβαδόν του τριγώνου
. Υπολογίστε την περίμετρο και το εμβαδόν του τριγώνου  .
.
 και
και  εφάπτονται εξωτερικά στο
εφάπτονται εξωτερικά στο  . Εντοπίστε σημεία
. Εντοπίστε σημεία  , των δύο
, των δύο .
.
 . Ας είναι
. Ας είναι  το μέσο της διαμέσου
το μέσο της διαμέσου  και
και  η προβολή του
η προβολή του  στην
στην  .
. είναι εγγράψιμο σε κύκλο .
είναι εγγράψιμο σε κύκλο . , θεωρούμε χορδή :
, θεωρούμε χορδή :  . Υπολογίστε την διχοτόμο
. Υπολογίστε την διχοτόμο  .
.
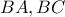 του - πλευράς
του - πλευράς  - ισοπλεύρου τριγώνου
- ισοπλεύρου τριγώνου  αντίστοιχα , τέτοια ώστε :
αντίστοιχα , τέτοια ώστε :  . Αν
. Αν  και η
και η 
 στο σημείο
στο σημείο  , υπολογίστε το τμήμα
, υπολογίστε το τμήμα  .
.
 ,
,  . Υπολογίστε την
. Υπολογίστε την  , είναι εγγεγραμμένο σε κύκλο
, είναι εγγεγραμμένο σε κύκλο  .
. προεκτεινόμενη , τέμνει την
προεκτεινόμενη , τέμνει την  .
.
 . Αν χρησιμοποιήσετε υπολογισμούς , θα πρέπει να βρείτε και την
. Αν χρησιμοποιήσετε υπολογισμούς , θα πρέπει να βρείτε και την  .
.
 , το σημείο
, το σημείο  είναι η προβολή του
είναι η προβολή του  . Για ποιο είδος ορθογωνίου προκύπτει :
. Για ποιο είδος ορθογωνίου προκύπτει :  ;
;
 του τραπεζίου του σχήματος . Αν :
του τραπεζίου του σχήματος . Αν :  , υπολογίστε το
, υπολογίστε το  .
.
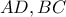 του τραπεζίου
του τραπεζίου 
 , τέτοιο ώστε :
, τέτοιο ώστε :  . Η
. Η 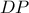 τέμνει την
τέμνει την  στο σημείο
στο σημείο  ,
, .
. . Υπολογίστε το τμήμα
. Υπολογίστε το τμήμα  .
.