Η αναζήτηση βρήκε 17044 εγγραφές
Επιστροφή στην ειδική αναζήτηση
- Πέμ Ιαν 22, 2026 9:31 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Juniors)
- Θέμα: Η άλλη κάθετη
- Απαντήσεις: 1
- Προβολές: 12
Η άλλη κάθετη
Η άλλη κάθετη.png Σε ορθογώνιο $ABCD$ , διαστάσεων $m \times n$ , έστω $E$ τυχόν σημείο της $AB$ . Εντοπίστε σημείο $Z$ της $AD$ , τέτοιο ώστε να είναι : $(ZDC)=(AZE)+(CEB)$ , δηλαδή βρείτε το $AZ$ συναρτήσει του $AE=x$ . Η άσκηση είναι προφανώς εμπνευσμένη από το αναπάντητο ακόμα θέμα του Ανδρέα Β...
- Πέμ Ιαν 22, 2026 7:43 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Juniors)
- Θέμα: Εξέχον τμήμα 3
- Απαντήσεις: 1
- Προβολές: 27
Εξέχον τμήμα 3
Εξέχον τμήμα 3.png Το $AD$ είναι το προς την υποτείνουσα ύψος του ορθογωνίου τριγώνου $ABC$ . Ο κύκλος διαμέτρου $AD$ τέμνει τις $AB , AC$ στα σημεία $P ,T$ , ενώ οι προεκτάσεις των $PT , BC$ , τέμνονται στο σημείο $S$ . Υπολογίστε το τμήμα $CS=x$ , συναρτήσει των $BD=y$ και $DC = z$ . Εφαρμογή : $...
- Τετ Ιαν 21, 2026 9:32 pm
- Δ. Συζήτηση: Γενικά - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Απαιτητικός κύκλος
- Απαντήσεις: 7
- Προβολές: 177
Re: Απαιτητικός κύκλος
Η λύση Φραγκάκη , έχει μοναδικό αλλά σημαντικό μειονέκτημα : Τα σημεία του σχήματος έχουν διαστάσεις 
- Τετ Ιαν 21, 2026 10:58 am
- Δ. Συζήτηση: ΜΑΘΗΜΑΤΙΚΑ ΚΑΤΕΥΘΥΝΣΗΣ Β'
- Θέμα: Προσβάσιμος τόπος
- Απαντήσεις: 1
- Προβολές: 76
Προσβάσιμος τόπος
Το  είναι σταθερό σημείο του
είναι σταθερό σημείο του  , ενώ το
, ενώ το  κινείται στον
κινείται στον  . Σε ημιευθεία η οποία
. Σε ημιευθεία η οποία
σχηματίζει με τον οριζόντιο άξονα θετική γωνία ίση μα την , θεωρούμε σημείο
, θεωρούμε σημείο  ,
,
τέτοιο ώστε : . Βρείτε τον γεωμετρικό τόπο του σημείου
. Βρείτε τον γεωμετρικό τόπο του σημείου  .
.
 είναι σταθερό σημείο του
είναι σταθερό σημείο του  , ενώ το
, ενώ το  κινείται στον
κινείται στον  . Σε ημιευθεία η οποία
. Σε ημιευθεία η οποίασχηματίζει με τον οριζόντιο άξονα θετική γωνία ίση μα την
 , θεωρούμε σημείο
, θεωρούμε σημείο  ,
,τέτοιο ώστε :
 . Βρείτε τον γεωμετρικό τόπο του σημείου
. Βρείτε τον γεωμετρικό τόπο του σημείου  .
.- Τετ Ιαν 21, 2026 8:35 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Juniors)
- Θέμα: Ισότητα ασχέτων
- Απαντήσεις: 1
- Προβολές: 49
Ισότητα ασχέτων
Ισότητα ασχέτων.png Στο ορθογώνιο τρίγωνο $ABC$ , η κάθετη πλευρά $AC$ έχει μήκος $4$ , ενώ η $AB$ έχει μεταβλητό μήκος . Στην προέκταση της $AB$ θεωρούμε σημείο $K$ , τέτοιο ώστε : $BK=2$ και γράφω τον κύκλο $(K , KB)$ , προς τον οποίο φέρω το εφαπτόμενο τμήμα $CS=m$ . Δείξτε ότι το εμβαδόν του τε...
- Τετ Ιαν 21, 2026 6:18 am
- Δ. Συζήτηση: Γενικά - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Απαιτητικός κύκλος
- Απαντήσεις: 7
- Προβολές: 177
Απαιτητικός κύκλος
Με κέντρο το σημείο  να γραφεί κύκλος , ο οποίος να τέμνει τις πλευρές
να γραφεί κύκλος , ο οποίος να τέμνει τις πλευρές 
του τριγώνου , σε σημεία
, σε σημεία  αντίστοιχα , έτσι ώστε να είναι :
αντίστοιχα , έτσι ώστε να είναι :  .
.
 να γραφεί κύκλος , ο οποίος να τέμνει τις πλευρές
να γραφεί κύκλος , ο οποίος να τέμνει τις πλευρές 
του τριγώνου
 , σε σημεία
, σε σημεία  αντίστοιχα , έτσι ώστε να είναι :
αντίστοιχα , έτσι ώστε να είναι :  .
.- Τρί Ιαν 20, 2026 6:54 pm
- Δ. Συζήτηση: Γενικά - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Τριτρόπως
- Απαντήσεις: 3
- Προβολές: 94
Τριτρόπως
Εντοπίστε το σημείο  της ευθείας
της ευθείας 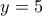 , για το οποίο είναι :
, για το οποίο είναι :  .
.
 της ευθείας
της ευθείας 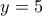 , για το οποίο είναι :
, για το οποίο είναι :  .
.- Τρί Ιαν 20, 2026 11:32 am
- Δ. Συζήτηση: Γεωμετρία
- Θέμα: Ούτε είκοσι
- Απαντήσεις: 1
- Προβολές: 138
Ούτε είκοσι
Με το σημείο  χωρίσαμε το τμήμα
χωρίσαμε το τμήμα  σε μέρη :
σε μέρη : 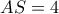 και
και  . Με διαμέτρους τις
. Με διαμέτρους τις 
γράψαμε στο ίδιο ημιεπίπεδο δύο ημικύκλια , επί των οποίων κινούνται σημεία . Μπορούμε άραγε
. Μπορούμε άραγε
να υπολογίσουμε το μέγιστο εμβαδόν του τετραπλεύρου ;
;
 χωρίσαμε το τμήμα
χωρίσαμε το τμήμα  σε μέρη :
σε μέρη : 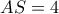 και
και  . Με διαμέτρους τις
. Με διαμέτρους τις 
γράψαμε στο ίδιο ημιεπίπεδο δύο ημικύκλια , επί των οποίων κινούνται σημεία
 . Μπορούμε άραγε
. Μπορούμε άραγε να υπολογίσουμε το μέγιστο εμβαδόν του τετραπλεύρου
 ;
;- Τρί Ιαν 20, 2026 10:01 am
- Δ. Συζήτηση: Γενικά - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Νεότοπος
- Απαντήσεις: 2
- Προβολές: 101
Νεότοπος
Στον ημιάξονα  είναι σταθερά τα σημεία
είναι σταθερά τα σημεία  . Μεταβλητή ημιευθεία του πρώτου τεταρτημορίου
. Μεταβλητή ημιευθεία του πρώτου τεταρτημορίου
τέμνει τα τεταρτοκύκλια με κέντρο και ακτίνες
και ακτίνες  και
και  στα σημεία
στα σημεία  αντίστοιχα .
αντίστοιχα .
Βρείτε τον γεωμετρικό τόπο του σημείου τομής των τμημάτων
των τμημάτων 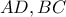 .
.
 είναι σταθερά τα σημεία
είναι σταθερά τα σημεία  . Μεταβλητή ημιευθεία του πρώτου τεταρτημορίου
. Μεταβλητή ημιευθεία του πρώτου τεταρτημορίου τέμνει τα τεταρτοκύκλια με κέντρο
 και ακτίνες
και ακτίνες  και
και  στα σημεία
στα σημεία  αντίστοιχα .
αντίστοιχα . Βρείτε τον γεωμετρικό τόπο του σημείου τομής
 των τμημάτων
των τμημάτων 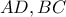 .
.- Δευ Ιαν 19, 2026 7:55 pm
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Έστω μία πλευρά
- Απαντήσεις: 3
- Προβολές: 108
Re: Έστω μία πλευρά
Πρόσθετο ερώτημα : Ποια ιδιότητα πρέπει να έχει το τρίγωνο  , ώστε το
, ώστε το  να είναι ισοσκελές ;
να είναι ισοσκελές ;
 , ώστε το
, ώστε το  να είναι ισοσκελές ;
να είναι ισοσκελές ;- Δευ Ιαν 19, 2026 5:54 pm
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Έστω μία πλευρά
- Απαντήσεις: 3
- Προβολές: 108
Έστω μία πλευρά
Η  είναι διχοτόμος στο τρίγωνο
είναι διχοτόμος στο τρίγωνο  και το
και το  σημείο της
σημείο της  , τέτοιο ώστε :
, τέτοιο ώστε :  .
.
Αν το έχει περίμετρο
έχει περίμετρο  και το
και το  περίμετρο
περίμετρο  , υπολογίστε μια πλευρά του
, υπολογίστε μια πλευρά του  .
.
 είναι διχοτόμος στο τρίγωνο
είναι διχοτόμος στο τρίγωνο  και το
και το  σημείο της
σημείο της  , τέτοιο ώστε :
, τέτοιο ώστε :  .
.Αν το
 έχει περίμετρο
έχει περίμετρο  και το
και το  περίμετρο
περίμετρο  , υπολογίστε μια πλευρά του
, υπολογίστε μια πλευρά του  .
.- Δευ Ιαν 19, 2026 10:11 am
- Δ. Συζήτηση: Διασκεδαστικά Μαθηματικά
- Θέμα: Είπες παραλληλεπίπεδο ή παραλληλόγραμμο;
- Απαντήσεις: 1
- Προβολές: 103
Re: Είπες παραλληλεπίπεδο ή παραλληλόγραμμο;
Από το  άρι ορθογώνιο έχουμε :
άρι ορθογώνιο έχουμε :  . Αλλά :
. Αλλά :  .
.
Αλλιώς : Το δίνει
δίνει  άρα το
άρα το  δίνει
δίνει  , συνεπώς :
, συνεπώς :  .
.
 άρι ορθογώνιο έχουμε :
άρι ορθογώνιο έχουμε :  . Αλλά :
. Αλλά :  .
. Αλλιώς : Το
 δίνει
δίνει  άρα το
άρα το  δίνει
δίνει  , συνεπώς :
, συνεπώς :  .
.- Δευ Ιαν 19, 2026 9:33 am
- Δ. Συζήτηση: Γεωμετρία
- Θέμα: Εξωτερική επαφή
- Απαντήσεις: 1
- Προβολές: 78
Εξωτερική επαφή
Τριγωνομετρική Γεωμετρία.png Η ημιευθεία $Oz$ είναι η διχοτόμος της γωνίας $\widehat{xOy}$ , ενώ η $Ot$ είναι η διχοτόμος της $\widehat{xOz}$ . Θεωρούμε σημεία $K$ της $Oz$ και $L$ της $Ot$ , τέτοια ώστε : $OL=2OK$ και γράφουμε τους κύκλους $(K) , (L)$ οι οποίοι εφάπτονται των πλευρών των γωνιών $\...
- Σάβ Ιαν 17, 2026 3:25 am
- Δ. Συζήτηση: ΕΥΚΛΕΙΔΕΙΑ ΓΕΩΜΕΤΡΙΑ Α'
- Θέμα: Αναπάντεχη ισότητα
- Απαντήσεις: 2
- Προβολές: 160
Αναπάντεχη ισότητα
 Με αρχή το σημείο
Με αρχή το σημείο  ενός κύκλου σχεδιάζουμε δύο χορδές του
ενός κύκλου σχεδιάζουμε δύο χορδές του  και
και  .
.Η κάθετη
 από το
από το  προς την
προς την  , τέμνει τον κύκλο στο
, τέμνει τον κύκλο στο  , ενώ η κάθετη
, ενώ η κάθετη 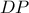 από το
από το  προς την
προς την  , τέμνει την
, τέμνει την  στο
στο  . Δείξτε ότι :
. Δείξτε ότι :  ,
,- Παρ Ιαν 16, 2026 7:50 pm
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Ενάρετος ημίκυκλος
- Απαντήσεις: 3
- Προβολές: 162
Ενάρετος ημίκυκλος
Ενάρετος ημίκυκλος.png Στο ημικύκλιο διαμέτρου $AOB=2r$ , το $N$ είναι το μέσο του τόξου , ενώ το $M$ είναι το μέσο της $ON$. Η διχοτόμος της γωνίας $\widehat{BAC}$ διέρχεται από το $M$ και τέμνει την $BC$ στο $L$ και το τόξο στο $S$ . Επίσης η $CB$ τέμνει την $ON$ στο $P$ ... α) Δείξτε ότι : $\dfr...
- Παρ Ιαν 16, 2026 3:32 pm
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Juniors)
- Θέμα: Απλά διπλάσιο
- Απαντήσεις: 2
- Προβολές: 103
Re: Απλά διπλάσιο
Μια άλλη λύση στο συνημμένο σχήμα :
- Παρ Ιαν 16, 2026 2:59 pm
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Juniors)
- Θέμα: Διπλό διπλάσιο
- Απαντήσεις: 7
- Προβολές: 195
Re: Διπλό διπλάσιο
Θα μπορούσαμε επίσης να χρησιμοποιήσουμε την πρόταση : " Το συμμετρικό του ορθοκέντρου ως προς
την βάση είναι σημείο του περικύκλου " . Το σημείο είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  .
.
την βάση είναι σημείο του περικύκλου " . Το σημείο
 είναι το ορθόκεντρο του τριγώνου
είναι το ορθόκεντρο του τριγώνου  .
.- Παρ Ιαν 16, 2026 11:02 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Παράκυκλος
- Απαντήσεις: 4
- Προβολές: 122
Re: Παράκυκλος
Παράκυκλος.png Αφού ευχαριστήσω τους τρεις δεινούς λύτες ( κυρίως για το κουράγιο τους λόγω των αρκετών πράξεων ) , παραθέτω και την δική μου επίσης επίπονη ( τριγωνομετρική ) λύση , χωρίς τις ανιαρές πράξεις : Είναι : $r=\dfrac{AD}{2\sin\theta} = \dfrac{5\sin B}{2\sin(B-C)}$ . Αλλά είναι : $\dfrac...
- Παρ Ιαν 16, 2026 9:01 am
- Δ. Συζήτηση: Γεωμετρία - Επίπεδο Θαλή/Ευκλείδη (Juniors)
- Θέμα: Νέο εμβαδόν
- Απαντήσεις: 4
- Προβολές: 104
Νέο εμβαδόν
Νέο εμβαδόν.png Σε ορθογώνιο τρίγωνο $ABC$ με κάθετες πλευρές $AC=b $ και $AB=c$ , σημείο $S$ κινείται στην $AB$ . Η κάθετη της $CS$ στο $S$ και η κάθετη της $CB$ στο $B$ , τέμνονται στο σημείο $T$ . Υπολογίστε το εμβαδόν του τριγώνου $TSB$ , συναρτήσει του $x$ . Εφαρμογή : $b=5 , c=8 , x=3$ .
- Παρ Ιαν 16, 2026 7:03 am
- Δ. Συζήτηση: ΔΙΑΦΟΡΙΚΟΣ ΛΟΓΙΣΜΟΣ
- Θέμα: Ισότητα αγνώστων
- Απαντήσεις: 1
- Προβολές: 93
Ισότητα αγνώστων
Ισότητα αγνώστων.png $\bigstar$ Από το σημείο $S(-3,6)$ διέρχεται ευθεία η οποία τέμνει τους ημιάξονες $Oy , Ox$ στα σημεία $B,A$ αντίστοιχα . α) Βρείτε τον γεωμετρικό τόπο του μέσου $M$ του τμήματος $AB$ . β) Η εφαπτομένη της καμπύλης ( που είναι ο παραπάνω τόπος ) , στο σημείο $M$ , τέμνει τον $O...
