Η αναζήτηση βρήκε 600 εγγραφές
Επιστροφή στην ειδική αναζήτηση
- Τρί Απρ 29, 2025 1:28 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Διαφορικὴ ἐξίσωση πεπλεγμένης μορφῆς
- Απαντήσεις: 2
- Προβολές: 1439
Διαφορικὴ ἐξίσωση πεπλεγμένης μορφῆς
Πρόβλημα. Ἔστω διαφορίσιμη συνάρτηση $f:\mathbb R\to\mathbb R$, ὥστε $|f'(x)|=|f{(x)|,$ διὰ κάθε $x\in\mathbb R$. Τότε συμβαίνει ἀκριβῶς ἕνα ἀπὸ τὰ κάτωθι: $(i)$ Ἡ $f$ εἶναι ταυτοτικῶς μηδενική. $(ii)$ Ὑπάρχει $c\ne 0,$ ὥστε $f(x)=c e^x$, διὰ κάθε $x\in\mathbb R$. $(iii)$ Ὑπάρχει $c\ne 0,$ ὥστε $f(...
- Κυρ Απρ 27, 2025 9:42 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Τρίτη παράγωγος ταυτοτικῶς μηδενική
- Απαντήσεις: 3
- Προβολές: 1413
Re: Τρίτη παράγωγος ταυτοτικῶς μηδενική
Γενικεύεται περαιτέρω:
Ἂν ἄπειρες φορές παραγωγίσιμη συνάρτηση, ὥστε διὰ κάθε
ἄπειρες φορές παραγωγίσιμη συνάρτηση, ὥστε διὰ κάθε 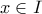 , ὑπάρχει
, ὑπάρχει  , ὥστε
, ὥστε
 , τότε ἡ
, τότε ἡ  εἶναι πολυώνυμο.
εἶναι πολυώνυμο.
Ἂν
 ἄπειρες φορές παραγωγίσιμη συνάρτηση, ὥστε διὰ κάθε
ἄπειρες φορές παραγωγίσιμη συνάρτηση, ὥστε διὰ κάθε 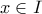 , ὑπάρχει
, ὑπάρχει  , ὥστε
, ὥστε , τότε ἡ
, τότε ἡ  εἶναι πολυώνυμο.
εἶναι πολυώνυμο.- Κυρ Απρ 27, 2025 9:36 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Ὅριο ἀνάμεσα στὸ κατώτερο καὶ ἀνώτερο ὅριο
- Απαντήσεις: 2
- Προβολές: 1913
Ὅριο ἀνάμεσα στὸ κατώτερο καὶ ἀνώτερο ὅριο
Πρόβλημα. Ἔστω  συνεχὴς, καὶ ἔστω
συνεχὴς, καὶ ἔστω

Δείξατε ὅτι ὑπάρχει καὶ αύξουσα ἀκολουθία ἀκεραίων
καὶ αύξουσα ἀκολουθία ἀκεραίων  , ὥστε
, ὥστε  .
.
 συνεχὴς, καὶ ἔστω
συνεχὴς, καὶ ἔστω
Δείξατε ὅτι ὑπάρχει
 καὶ αύξουσα ἀκολουθία ἀκεραίων
καὶ αύξουσα ἀκολουθία ἀκεραίων  , ὥστε
, ὥστε  .
.- Σάβ Απρ 26, 2025 3:02 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Ὀλοκληρωτικὴ ἀνίσωση
- Απαντήσεις: 1
- Προβολές: 1910
Ὀλοκληρωτικὴ ἀνίσωση
Πρόβλημα. Ἔστω ![f:[0,1]\to\mathbb R f:[0,1]\to\mathbb R](/forum/ext/geomar/texintegr/latexrender/pictures/2b80fa95661cd96d5ba60c3aa700e464.png) συνεχὴς καὶ
συνεχὴς καὶ  . Ἂν
. Ἂν

διὰ κάθε![x\in[0,1] x\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ee73e01397b466fca4731317471bd6ff.png) , δείξατε ὅτι
, δείξατε ὅτι  .
.
![f:[0,1]\to\mathbb R f:[0,1]\to\mathbb R](/forum/ext/geomar/texintegr/latexrender/pictures/2b80fa95661cd96d5ba60c3aa700e464.png) συνεχὴς καὶ
συνεχὴς καὶ  . Ἂν
. Ἂν
διὰ κάθε
![x\in[0,1] x\in[0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ee73e01397b466fca4731317471bd6ff.png) , δείξατε ὅτι
, δείξατε ὅτι  .
.- Σάβ Απρ 26, 2025 1:45 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Τρίτη παράγωγος ταυτοτικῶς μηδενική
- Απαντήσεις: 3
- Προβολές: 1413
Τρίτη παράγωγος ταυτοτικῶς μηδενική
Πρόβλημα. Ἔστω  τρὶς παραγωγίσιμη. Ἄν
τρὶς παραγωγίσιμη. Ἄν  διὰ κάθε
διὰ κάθε  , δείξατε ὅτι
, δείξατε ὅτι  .
.
 τρὶς παραγωγίσιμη. Ἄν
τρὶς παραγωγίσιμη. Ἄν  διὰ κάθε
διὰ κάθε  , δείξατε ὅτι
, δείξατε ὅτι  .
.- Παρ Απρ 18, 2025 2:51 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Μονοτονία λύσεων αὐτονόμων ἐξισώσεων μὲ ὁμαλὴ συνάρτηση ροῆς
- Απαντήσεις: 2
- Προβολές: 713
Re: Μονοτονία λύσεων αὐτονόμων ἐξισώσεων
Μιχάλη, πράγματι ἡ συνεχὴς διαφορισιμότης τῆς  ἐξασφαλίζει καθολικὴ μοναδικότητα, καὶ αὐτὸ εἶναι τὸ κλειδί!
ἐξασφαλίζει καθολικὴ μοναδικότητα, καὶ αὐτὸ εἶναι τὸ κλειδί!
 ἐξασφαλίζει καθολικὴ μοναδικότητα, καὶ αὐτὸ εἶναι τὸ κλειδί!
ἐξασφαλίζει καθολικὴ μοναδικότητα, καὶ αὐτὸ εἶναι τὸ κλειδί!- Παρ Απρ 18, 2025 2:49 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Μονοτονία λύσεων αὐτονόμων ἐξισώσεων
- Απαντήσεις: 2
- Προβολές: 1508
Re: Μονοτονία λύσεων αὐτονόμων ἐξισώσεων
Παραθέτω λύση μετὰ ἀπὸ σχεδὸν 8 χρόνια! Ἔστω ὅτι ἡ συνἀρτηση $f: J\to\mathbb R$ εἶναι συνεχής, ὅπου $J$ ἀνοικτὸ διάστημα, καὶ ἔστω $\varphi : I\to\mathbb R,$ λύση τῆς ἐξισώσεως $x'=f(x),$ ὅπου $I$ ἀνοικτὸ διάστημα. Νὰ ἀποδειχθεῖ ὅτι ἡ $\varphi$ εἶναι μονότονη. Ἀπόδειξη. Ἂν ἡ $\varphi$ δὲν εἶναι μονό...
- Τετ Απρ 16, 2025 11:32 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Μονοτονία λύσεων αὐτονόμων ἐξισώσεων μὲ ὁμαλὴ συνάρτηση ροῆς
- Απαντήσεις: 2
- Προβολές: 713
Μονοτονία λύσεων αὐτονόμων ἐξισώσεων μὲ ὁμαλὴ συνάρτηση ροῆς
[b]Πρόταση.[/b] Ἔστω  συνεχῶς διαφορίσιμη, καὶ
συνεχῶς διαφορίσιμη, καὶ  ὅπου
ὅπου  ἀνοικτὸ διάστημα, λύση τῆς ἐξισώσεως
ἀνοικτὸ διάστημα, λύση τῆς ἐξισώσεως  . Τότε ἡ
. Τότε ἡ  εἴτε εἶναι γνησίως μονότονη στὸ
εἴτε εἶναι γνησίως μονότονη στὸ  εἴτε σταθερή στὸ
εἴτε σταθερή στὸ  .
.
 συνεχῶς διαφορίσιμη, καὶ
συνεχῶς διαφορίσιμη, καὶ  ὅπου
ὅπου  ἀνοικτὸ διάστημα, λύση τῆς ἐξισώσεως
ἀνοικτὸ διάστημα, λύση τῆς ἐξισώσεως  . Τότε ἡ
. Τότε ἡ  εἴτε εἶναι γνησίως μονότονη στὸ
εἴτε εἶναι γνησίως μονότονη στὸ  εἴτε σταθερή στὸ
εἴτε σταθερή στὸ  .
.- Τετ Απρ 16, 2025 11:19 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Λύσεις τῆς ἰδίας αὐτόνομης ἐξισώσεως
- Απαντήσεις: 2
- Προβολές: 802
Re: Λύσεις τῆς ἰδίας αὐτόνομης ἐξισώσεως
Δυστυχῶς ἡ διατύπωση τοῦ προβλήματος μου εἶχε μία παράλειψη, καὶ συγκεκριμένα ὅτι ἡ λύση $\color{red}\varphi:\mathbb R\to\mathbb R$ εἶναι ἐπί. Σὲ αὐτὴ τὴν περίπτωση, ὑπάρχει $\tau\in\mathbb R,$ ὥστε $\displaystyle{ \varphi(\tau)=\psi(0)=\xi. }$ Ἐπίσης, ἂν $\zeta(t)=\psi(t-\tau),$ τότε οἱ συναρτήσεις...
- Δευ Απρ 14, 2025 7:47 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Ταχύτητα συγκλίσεως ακολουθίας
- Απαντήσεις: 8
- Προβολές: 1253
Re: Ταχύτητα συγκλίσεως ακολουθίας
Ὑπόδειξη (γιὰ τὴν ἀπόδειξη ποὺ ἔχω ὑπόψη.)
Χρησιμοποιῆστε τὸ Cauchy Condensation Test https://en.wikipedia.org/wiki/Cauchy_condensation_test δύο φορές, ὁπότε ἡ σειρὰ

συγκλίνει, ὅπου .
.
Χρησιμοποιῆστε τὸ Cauchy Condensation Test https://en.wikipedia.org/wiki/Cauchy_condensation_test δύο φορές, ὁπότε ἡ σειρὰ

συγκλίνει, ὅπου
 .
.- Δευ Απρ 14, 2025 1:26 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Ἀνισες λύσεις αυτόνομης εξισώσεως
- Απαντήσεις: 1
- Προβολές: 702
Ἀνισες λύσεις αυτόνομης εξισώσεως
Πρόβλημα. Ἔστω ὅτι οἱ συναρτήσεις  ἀποτελοῦν λύσεις τῆς διαφορικῆς ἐξισώσεως
ἀποτελοῦν λύσεις τῆς διαφορικῆς ἐξισώσεως  καὶ ἔστω ὅτι
καὶ ἔστω ὅτι  ἐνῶ
ἐνῶ  Δεἰξατε ὅτι
Δεἰξατε ὅτι

διὰ κάθε .
.
 ἀποτελοῦν λύσεις τῆς διαφορικῆς ἐξισώσεως
ἀποτελοῦν λύσεις τῆς διαφορικῆς ἐξισώσεως  καὶ ἔστω ὅτι
καὶ ἔστω ὅτι  ἐνῶ
ἐνῶ  Δεἰξατε ὅτι
Δεἰξατε ὅτι 
διὰ κάθε
 .
.- Δευ Απρ 14, 2025 1:17 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Λύσεις τῆς ἰδίας αὐτόνομης ἐξισώσεως
- Απαντήσεις: 2
- Προβολές: 802
Λύσεις τῆς ἰδίας αὐτόνομης ἐξισώσεως
Τροποποίηση τοῦ προηγούμενου θέματος, προσθέτοντας μία ἰδιότητα στὴν $f$ καὶ ἀφαιρῶντας μία ἄλλη: Πρόβλημα. Ἔστω ὅτι οἱ συναρτήσεις $\varphi,\psi : \mathbb R\to\mathbb R,$ ἀποτελοῦν λύσεις τῆς διαφορικῆς ἐξισώσεως $x'=f(x),$ ὅπου $f:\mathbb R\to\mathbb R,$ συνεχῶς διαφορίσιμη. Δείξατε ὅτι ὑπάρχει $\...
- Δευ Απρ 14, 2025 1:04 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Δύο λύσεις της ίδιας ΣΔΕ
- Απαντήσεις: 2
- Προβολές: 716
Re: Δύο λύσεις της ίδιας ΣΔΕ
Χαιρετίσματα στην Κρήτη.
- Κυρ Απρ 13, 2025 3:08 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Δύο λύσεις της ίδιας ΣΔΕ
- Απαντήσεις: 2
- Προβολές: 716
Δύο λύσεις της ίδιας ΣΔΕ
Πρόβλημα. Ἔστω ὅτι οἱ συναρτήσεις $\varphi,\psi : \mathbb R\to\mathbb R,$ ἀποτελοῦν λύσεις τῆς διαφορικῆς ἐξισώσεως $x'=f(x),$ ὅπου $f:\mathbb R\to\mathbb R,$ συνεχὴς καὶ $f(x)\ne 0,$ διὰ κάθε $x\in\mathbb R$. Δείξατε ὅτι ὑπάρχει $\tau\in\mathbb R,$ ὥστε $\displaystyle{ \psi(t)=\varphi(t-\tau), }$ ...
- Κυρ Απρ 13, 2025 2:43 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: 1-1 στὸ σύνορο έπεται 1-1 στο ἐσωτερικό
- Απαντήσεις: 1
- Προβολές: 741
Re: 1-1 στὸ σύνορο έπεται 1-1 στο ἐσωτερικό
Ἀπόδειξη. Ἔστω $\gamma_r(t)=f(re^{it}),$ ὅπου $\,t\in [0,2\pi]$, καὶ $\,r\in (0,1]$. Καθὼς ἡ $f$ εἶναι ἐξ ὑποθέσεως ἕνα-πρὸς-ἕνα, ὅταν περιορισθεῖ στὸν μοναδιαῖο κύκλο, τότε ἡ $\gamma_1$ εἶναι ἁπλὴ κλειστὴ καμπύλη. Σύμφωνα μὲ τὸ Θεώρημα τῆς Καμπύλης Jordan , τὸ συμπλήρωμά τῆς $\gamma_1$ ἀποτελεῖται...
- Σάβ Απρ 12, 2025 11:18 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Ταχύτητα συγκλίσεως ακολουθίας
- Απαντήσεις: 8
- Προβολές: 1253
Re: Ταχύτητα συγκλίσεως ακολουθίας
Ἡ ὑπόθεση ὅτι ἡ  εἶναι φθίνουσα, ΔΕΝ συνεπάγεται ὅτι καὶ ἡ
εἶναι φθίνουσα, ΔΕΝ συνεπάγεται ὅτι καὶ ἡ  εἶναι ἐπίσης φθίνουσα!
εἶναι ἐπίσης φθίνουσα!
 εἶναι φθίνουσα, ΔΕΝ συνεπάγεται ὅτι καὶ ἡ
εἶναι φθίνουσα, ΔΕΝ συνεπάγεται ὅτι καὶ ἡ  εἶναι ἐπίσης φθίνουσα!
εἶναι ἐπίσης φθίνουσα!- Τρί Απρ 08, 2025 1:10 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Όριο ολοκληρώματος με συνημίτονο
- Απαντήσεις: 8
- Προβολές: 1750
Re: Όριο ολοκληρώματος με συνημίτονο
Γενίκευση:


- Κυρ Απρ 06, 2025 2:46 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Γενικευμένη εκδοχή του Θεωρήματος Ενδιαμέσου Τιμής
- Απαντήσεις: 0
- Προβολές: 710
Γενικευμένη εκδοχή του Θεωρήματος Ενδιαμέσου Τιμής
Πρόβλημα. Ἔστω $f:[0,1]\to\mathbb R^2$ συνεχὴς συνάρτηση, ὥστε $\displaystyle{ f(1)-f(0) = (1,0). }$ Δείξατε ὅτι διὰ κάθε $n\in\mathbb N,$ ὑπάρχουν $t_1,t_2\in [0,1]$, ὥστε $f(t_2)-f(t_1)=(1/n,0)$. Τὸ ἀνωτέρω ἔχει τὸ ἑξῆς πόρισμα: Πόρισμα. Ἔστω $\gamma : [0,1]\to\mathbb R^2$ κλειστὴ καμπύλη, $\gamm...
- Κυρ Απρ 06, 2025 2:10 pm
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Ταχύτητα συγκλίσεως ακολουθίας
- Απαντήσεις: 8
- Προβολές: 1253
Re: Ταχύτητα συγκλίσεως ακολουθίας
Ἡ σύγκλιση της σειρᾶς  ἀποτελεῖ ὑποθεση!
ἀποτελεῖ ὑποθεση!
Οἱ ὑποθέσεις φθίνουσα καὶ
φθίνουσα καὶ  συγκλίνουσα , ἔχουν ὡς συνέπεια ὅτι
συγκλίνουσα , ἔχουν ὡς συνέπεια ὅτι  .
.
Ἡ σίγουρα δὲν ἀποτελεῖ ἀντιπαράδειγμα!
σίγουρα δὲν ἀποτελεῖ ἀντιπαράδειγμα!
 ἀποτελεῖ ὑποθεση!
ἀποτελεῖ ὑποθεση!Οἱ ὑποθέσεις
 φθίνουσα καὶ
φθίνουσα καὶ  συγκλίνουσα , ἔχουν ὡς συνέπεια ὅτι
συγκλίνουσα , ἔχουν ὡς συνέπεια ὅτι  .
.Ἡ
 σίγουρα δὲν ἀποτελεῖ ἀντιπαράδειγμα!
σίγουρα δὲν ἀποτελεῖ ἀντιπαράδειγμα!- Σάβ Απρ 05, 2025 3:18 am
- Δ. Συζήτηση: ΑΝΑΛΥΣΗ
- Θέμα: Ταχύτητα συγκλίσεως ακολουθίας
- Απαντήσεις: 8
- Προβολές: 1253
Ταχύτητα συγκλίσεως ακολουθίας
Πρόβλημα. Ἔστω ὅτι ἡ ὅροι τῆς ἀκολουθίας  εἶναι θετικοὶ, καὶ ἔστω ἐπίσης ὅτι ἡ ἀκολουθία
εἶναι θετικοὶ, καὶ ἔστω ἐπίσης ὅτι ἡ ἀκολουθία  εἶναι φθίνουσα. Ἂν ἡ σειρὰ
εἶναι φθίνουσα. Ἂν ἡ σειρὰ  συγκλίνει, τότε δείξατε ὅτι
συγκλίνει, τότε δείξατε ὅτι

 εἶναι θετικοὶ, καὶ ἔστω ἐπίσης ὅτι ἡ ἀκολουθία
εἶναι θετικοὶ, καὶ ἔστω ἐπίσης ὅτι ἡ ἀκολουθία  εἶναι φθίνουσα. Ἂν ἡ σειρὰ
εἶναι φθίνουσα. Ἂν ἡ σειρὰ  συγκλίνει, τότε δείξατε ὅτι
συγκλίνει, τότε δείξατε ὅτι 
