Η αναζήτηση βρήκε 132 εγγραφές
Επιστροφή στην ειδική αναζήτηση
- Παρ Ιουν 09, 2017 6:53 pm
- Δ. Συζήτηση: Πανελλήνιες Εξετάσεις
- Θέμα: Σχόλια στα Μαθηματικά προσανατολισμού 2017
- Απαντήσεις: 99
- Προβολές: 26096
Re: Σχόλια στα Μαθηματικά προσανατολισμού 2017
Καλησπέρα θα ήθελα ως μαθητής να εκφράσω την ανησυχία μου :?: για τα σημερινά θέματα. Πάρα πολλές πράξεις χωρίς ουσία. Αλήθεια ποια είναι η διαφορά του Θέματος Β με το Θέμα Δ1,Δ2; Υπαρχει περίπτωση κάποιος μαθητής που μπορούσε να λύσει το Θέμα Δ1,Δ2 να μην μπορούσε να λύσει το Θέμα Β.Πραγματικα λύνο...
- Πέμ Μαρ 02, 2017 9:39 pm
- Δ. Συζήτηση: Συνδυαστική - Επίπεδο Αρχιμήδη (Seniors)
- Θέμα: Καραμέλες σε κουτιά
- Απαντήσεις: 8
- Προβολές: 2118
Re: Καραμέλες σε κουτιά
Καλησπέρα Κύριε Δημήτρη ευχαριστώ για την ενασχόληση σας! :D Λίγο διαφορετικά απο την δική σας προσέγγιση Θα αποδείξω ότι ισχύει για κάθε $n$ Θα κάνω επαγωγή στο αριθμό των καραμελών έστω $c$. Αρχικά για $c=4$, υπάρχουν το πολύ $4$ κουτία με καραμέλες. Οι πιθανές θέσεις των καραμελών στα μη άδεια κο...
- Πέμ Μαρ 02, 2017 3:48 pm
- Δ. Συζήτηση: Συνδυαστική - Επίπεδο Αρχιμήδη (Seniors)
- Θέμα: Καραμέλες σε κουτιά
- Απαντήσεις: 8
- Προβολές: 2118
Re: Καραμέλες σε κουτιά
Επαναφορά!(Μιας και ο Αρχιμήδης πλησιάζει)
- Δευ Φεβ 27, 2017 7:03 pm
- Δ. Συζήτηση: Θεωρία Αριθμών - Προχωρημένο Επίπεδο (Seniors)
- Θέμα: Ύπαρξη πρώτου και ακεραίου
- Απαντήσεις: 1
- Προβολές: 1593
Ύπαρξη πρώτου και ακεραίου
Να δειχθεί ότι για κάθε ακέραιο  που είναι είναι square free, υπάρχει πρώτος
που είναι είναι square free, υπάρχει πρώτος  και ακέραιος
και ακέραιος  έτσι ώστε:
έτσι ώστε:
 και
και 
 που είναι είναι square free, υπάρχει πρώτος
που είναι είναι square free, υπάρχει πρώτος  και ακέραιος
και ακέραιος  έτσι ώστε:
έτσι ώστε: και
και 
- Σάβ Φεβ 25, 2017 9:05 pm
- Δ. Συζήτηση: Συνδυαστική - Επίπεδο Αρχιμήδη (Seniors)
- Θέμα: Καραμέλες σε κουτιά
- Απαντήσεις: 8
- Προβολές: 2118
Re: Μπάλες σε κουτιά
Το τρίτο κουτί πρέπει να αλλάζει ή είναι σταθερό To τρίτο κουτί είναι τυχαίο. Το ζητούμενο μπορεί να επιτευχθεί για οποιοδήποτε$n$. Αν τοποθετήσουμε των απαραίτητο αριθμό καραμέλων κατάλληλα στα κουτιά Ο αριθμός των καραμελών είναι τυχαίος και έχουν τοποθετηθεί τυχαία στα κουτιά. Ξαναδιαβάστε πιο π...
- Σάβ Φεβ 25, 2017 6:09 pm
- Δ. Συζήτηση: Συνδυαστική - Επίπεδο Αρχιμήδη (Seniors)
- Θέμα: Καραμέλες σε κουτιά
- Απαντήσεις: 8
- Προβολές: 2118
Καραμέλες σε κουτιά
Καλησπέρα, μιας και ο Αρχιμήδης πλησιάζει προτείνω το παρακάτω, ελπίζοντας να ταυτίζεται με το επίπεδο του. Σε $n \geq 4$ κουτιά υπάρχουν (συνολικά) τουλάχιστον $4$ καραμέλες. Kάθε φορά ο Νίκος επιτρέπεται να διαλέξει $2$ κουτιά και να πάρει μία καραμέλα από το καθένα και να τις βάλει σε ένα τρίτο κ...
- Τρί Ιαν 10, 2017 10:32 pm
- Δ. Συζήτηση: Θεωρία Αριθμών - Προχωρημένο Επίπεδο (Seniors)
- Θέμα: Διοφαντική!!
- Απαντήσεις: 12
- Προβολές: 2908
Re: Διοφαντική!!
Ενώ ηΔιονύσιος Αδαμόπουλος έγραψε:Να βρεθούν όλες οι μη αρνητικές ακέραιες λύσεις της εξίσωσης
 πρόκειται για την εξίσωση του Ljunggren και η λύση της ξεφεύγει τελείως από την θεματική ενότητα.
πρόκειται για την εξίσωση του Ljunggren και η λύση της ξεφεύγει τελείως από την θεματική ενότητα.Καλό είναι πριν προτείνετε ασκήσεις να τις λύνεται πρώτα.
- Τετ Νοέμ 30, 2016 8:01 pm
- Δ. Συζήτηση: Άλγεβρα - Επίπεδο Θαλή/Ευκλείδη (Seniors)
- Θέμα: Πολυώνυμα - Συλλογή Ασκήσεων
- Απαντήσεις: 190
- Προβολές: 51910
Re: Πολυώνυμα - Συλλογή Ασκήσεων
ΑΣΚΗΣΗ 5
Καλησπέρα, προτείνω το παρακάτω:
Να βρεθούν όλα τα μη-σταθερά πραγματικά πολυώνυμα ώστε για κάθε
ώστε για κάθε  ισχύει:
ισχύει:

Καλησπέρα, προτείνω το παρακάτω:
Να βρεθούν όλα τα μη-σταθερά πραγματικά πολυώνυμα
 ώστε για κάθε
ώστε για κάθε  ισχύει:
ισχύει:
- Τετ Ιουν 22, 2016 12:07 pm
- Δ. Συζήτηση: Ασκήσεις ΜΟΝΟ για μαθητές
- Θέμα: Μέτρα διανυσμάτων
- Απαντήσεις: 6
- Προβολές: 2208
Re: Μέτρα διανυσμάτων
Γιώργος Ρίζος έγραψε: Οι υπόλοιποι θα ασχολούνται με τα απολύτως αναγκαία για την επιδοσή τους στις ενδοσχολικές εξετάσεις.
Aμφιβάλλω ακόμα και για αυτό
- Κυρ Μάιος 22, 2016 1:02 am
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Ανισότητα
- Απαντήσεις: 2
- Προβολές: 1139
Re: Ανισότητα
Eξαιρετικά 
Ας δούμε και την γενίκευση που δυστυχώς δεν έχω βρει κάποια προσέγγιση:
Έστω μη αρνητικοί πραγματικοί . Να δειχθεί ότι για κάθε πραγματικό
. Να δειχθεί ότι για κάθε πραγματικό 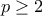 ισχύει:
ισχύει:

Ας δούμε και την γενίκευση που δυστυχώς δεν έχω βρει κάποια προσέγγιση:
Έστω μη αρνητικοί πραγματικοί
 . Να δειχθεί ότι για κάθε πραγματικό
. Να δειχθεί ότι για κάθε πραγματικό 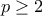 ισχύει:
ισχύει:
- Τετ Μάιος 18, 2016 7:25 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Ανισότητα
- Απαντήσεις: 2
- Προβολές: 1139
Ανισότητα
Kαλησπέρα σε όλους 
Ας δούμε μία ανισότητα που προσπάθησα να λύσω σήμερα:
Έστω μη αρνητικοί πραγματικοί αριθμοί . Να δειχθεί ότι:
. Να δειχθεί ότι:

Ας δούμε μία ανισότητα που προσπάθησα να λύσω σήμερα:
Έστω μη αρνητικοί πραγματικοί αριθμοί
 . Να δειχθεί ότι:
. Να δειχθεί ότι:
- Παρ Μαρ 11, 2016 5:00 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: 3 Ανισότητες
- Απαντήσεις: 5
- Προβολές: 888
Re: 3 Ανισότητες
Ας είναι $a,b,c > 0$ και $ab+bc+ca = 1$. Να δειχτεί ότι $\displaystyle{ \sqrt {a^3 + a} + \sqrt {b^3 + b} + \sqrt {c^3 + c}\geq2\sqrt {a + b + c}. }$ Αυτή δεν μου φαίνεται τόσο άμεση, όσο ήταν οι άλλες δύο: Γεια σας Κύριε Θάνο , ευχαριστώ για τον χρόνο σας, μάλλον έπρεπε να τα προτείνω στους junior...
- Παρ Μαρ 11, 2016 3:06 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: 3 Ανισότητες
- Απαντήσεις: 5
- Προβολές: 888
3 Ανισότητες
Ας είναι $a,b,c > 0$ και $ab+bc+ca = 1$. Να δειχτεί ότι $\displaystyle{ \sqrt {a^3 + a} + \sqrt {b^3 + b} + \sqrt {c^3 + c}\geq2\sqrt {a + b + c}. }$ $\displaystyle{a\sqrt {a^2 + 1} + b\sqrt {b^2 + 1} + c\sqrt {c^2 + 1}\geq2 ,}$ $\displaystyle{\sqrt {a^4 + b^2} + \sqrt {b^4 + c^2} + \sqrt {c^4 + a^2...
- Σάβ Μαρ 05, 2016 8:07 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Πάντα τέλειο τετράγωνο...
- Απαντήσεις: 7
- Προβολές: 1636
Re: Πάντα τέλειο τετράγωνο...
Can an infinite set of natural numbers be found, such that for all triplets $(a,b,c)$ of it we have $abc + 1$ perfect square? Αυτή είναι η αρχική εκφώνηση του προβλήματος πρόσθεσα ότι είναι διακεκριμένοι γιατί αλλιώς γίνεται πολύ απλό.Από ότι καταλαβαίνω εννοεί αυτό που λέτε ότι όλα τα στοιχεία είνα...
- Σάβ Μαρ 05, 2016 7:39 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Πάντα τέλειο τετράγωνο...
- Απαντήσεις: 7
- Προβολές: 1636
Re: Πάντα τέλειο τετράγωνο...
Kαλησπέρα το πρόβλημα δεν είναι δικό μου, είναι απο διεθνή διαγωνισμό
- Παρ Μαρ 04, 2016 8:58 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Πάντα τέλειο τετράγωνο...
- Απαντήσεις: 7
- Προβολές: 1636
Πάντα τέλειο τετράγωνο...
Να εξεταστεί εάν υπάρχει ένα σύνολο με άπειρους θετικούς ακεραίους, ώστε για κάθε διακεκριμένα  που ανήκουν σε αυτό ο αριθμός
που ανήκουν σε αυτό ο αριθμός  να είναι τέλειο τετράγωνο.
να είναι τέλειο τετράγωνο.
 που ανήκουν σε αυτό ο αριθμός
που ανήκουν σε αυτό ο αριθμός  να είναι τέλειο τετράγωνο.
να είναι τέλειο τετράγωνο.- Δευ Φεβ 22, 2016 6:41 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Juniors) - Παλαιότερες Συζητήσεις
- Θέμα: Βιβλία στο τραπέζι
- Απαντήσεις: 5
- Προβολές: 2089
Re: Βιβλία στο τραπέζι
Για να μην μείνει αναπάντητη , αν δεν κάνω κάποιο λάθος είναι πολύ απλή.
Έστω ότι τα μεγαλύτερα καλύπτουν λιγότερα από τα
μεγαλύτερα καλύπτουν λιγότερα από τα  τότε τα επόμενα
τότε τα επόμενα  θα καλύπτουν παραπάνω από τα
θα καλύπτουν παραπάνω από τα  . Άρα το ένατο μεγαλύτερο καλύπτει τουλάχιστον το
. Άρα το ένατο μεγαλύτερο καλύπτει τουλάχιστον το  .Άτοπο.
.Άτοπο.
Έστω ότι τα
 μεγαλύτερα καλύπτουν λιγότερα από τα
μεγαλύτερα καλύπτουν λιγότερα από τα  τότε τα επόμενα
τότε τα επόμενα  θα καλύπτουν παραπάνω από τα
θα καλύπτουν παραπάνω από τα  . Άρα το ένατο μεγαλύτερο καλύπτει τουλάχιστον το
. Άρα το ένατο μεγαλύτερο καλύπτει τουλάχιστον το  .Άτοπο.
.Άτοπο.- Κυρ Φεβ 14, 2016 11:43 pm
- Δ. Συζήτηση: Άλγεβρα - Θεωρία Αριθμών - Συνδυαστική (Seniors) - Παλαιότερες Συζητήσεις
- Θέμα: Vojtech Jarnik 1992/3 Category I
- Απαντήσεις: 2
- Προβολές: 572
Re: Vojtech Jarnik 1992/3 Category I
Ισχύει αφουDemetres έγραψε:Να δειχθεί για κάθεότι
 και
και 
- Κυρ Φεβ 14, 2016 11:40 pm
- Δ. Συζήτηση: Διαγωνισμοί για φοιτητές
- Θέμα: Vojtech Jarnik 1992/2 Category I
- Απαντήσεις: 4
- Προβολές: 816
Re: Vojtech Jarnik 1992/2 Category I
Καλησπέρα, όντως λίγο εύκολο αφού
 και
και  ικανοποιούν
ικανοποιούν
 και
και  ικανοποιούν
ικανοποιούν- Κυρ Φεβ 14, 2016 10:50 pm
- Δ. Συζήτηση: Διαγωνισμοί για φοιτητές
- Θέμα: IMC 2007/2/2
- Απαντήσεις: 3
- Προβολές: 775
Re: IMC 2007/2/2
Καλησπέρα , Κύριε Δημήτρη ψάχνοντας στο φάκελο βρήκα αυτό.
Αρχικά το βρήκα ενδιαφέρον αλλά μετά παρατήρησα:

H μόνη περίπτωση να πάρουμε είναι όλα να διαιρούνται από το
είναι όλα να διαιρούνται από το  και αφού το
και αφού το  είναι πρώτος το ζητούμενο αποδείχθηκε.
είναι πρώτος το ζητούμενο αποδείχθηκε.
Αρχικά το βρήκα ενδιαφέρον αλλά μετά παρατήρησα:

H μόνη περίπτωση να πάρουμε
 είναι όλα να διαιρούνται από το
είναι όλα να διαιρούνται από το  και αφού το
και αφού το  είναι πρώτος το ζητούμενο αποδείχθηκε.
είναι πρώτος το ζητούμενο αποδείχθηκε.

