Διάσταση χώρου Banach

Γ.-Σ. Σμυρλής · #1

Ἔστω

ἀπειροδιάστατος χῶρος Banach.

α. Δείξατε ὅτι $\mathrm{dim}\,X \ge 2^{\aleph_0}$ .

β. Ἄν ὁ

εἶναι διαχωρίσιμος, τότε $\mathrm{dim}\,X = 2^{\aleph_0}$ .

Σημείωση. Ἕνας χῶρος Banach εἶναι βεβαίως καί γραμμικός χῶρος ἐπί τοῦ $\mathbb R$ ἤ τοῦ $\mathbb C$ , καί ἀνωτέρω ἀναφερόμεθα στήν διάστασή του ὡς γραμμικοῦ χώρου.

kwstas12345 · #2

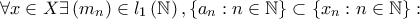
Δείχνουμε αρχικά ότιο ο χώρος έχει υπεραριθμήσιμη διάσταση, πράγματι αν αρνηθούμε το ζητούμενο , έστω $\displaystyle \left\{x_{n}:n\in \mathbb{N} \right\}$ μια αριθμήσιμη βάση Hammel.Tότε ορίζοντας $\displaystyle X_{n}:=\span\left\{x_{i}, 1\leq i\leq n \right\}$ , έχουμε ότι είναι κλειστοί υπόχωροι (αφού είναι πεπερασμένης διάστασης) και $\displaystyle \bigcup_{n=1}^{\infty}{X_{n}}=X$ .Λόγω πληρότητας από το θεώρημα Βaire υπάρχει γνήσιος υπόχωρος με μη κενό εσωτερικό, με αποτέλεσμα (γνωστή άσκηση) να είναι όλος ο χώρος, πράγμα άτοπο αφού έχει πεπερασμένη διάσταση.Άρα η $\dim X$ είναι υπεραριθμήσιμη, και χρησιμοποιώντας την υπόθεση του συνεχούς , έχουμε ότι $\displaystyle \dim X\geq 2^{\mathbb{N}}=\left|\mathbb{R} \right|$ .
Έστω τώρα ένα άπειρο αριθμήσιμο πυκνό $\displaystyle W=\left\{x_{n}:n\in \mathbb{N} \right\}\subset B_{X}$ .Tότε $\displaystyle \forall x\in X \exists \left(m_{n} \right)\in l_{1}\left(\mathbb{N} \right),\left\{a_{n}:n \in \mathbb{N} \right\}\subset \left\{x_{n}:n\in \mathbb{N} \right\}:$ $\displaystyle x=\sum_{n=1}^{\infty}{m_{n}a_{n}}$ . Πράγματι αν x=0

άμεσα ισχύει το ζητούμενο, αν

οχι

, τότε $\displaystyle \exists a_{1} \in W:\left|\left|\frac{x}{\left|\left|x \right| \right|} \right|-a_{1} \right|<1/2$ έπειτα $\displaystyle \exists a_{2}:\left|\left|u_{1}-a_{2} \right| \right|<1/2$ , με $\displaystyle u_{1}=2\left(\frac{x}{\left|\left|x \right| \right|}-a_{1} \right)$ .'Έπειτα υπάρχει $\displaystyle a_{3}:\left|\left|u_{2}-a_{3} \right| \right|<1/2, u_{2}=4\left(\frac{x}{\left|\left|x \right| \right|}-a_{1}-\frac{a_{2}}{2} \right)$ . Επαγωγικά βλέπουμε ότι υπάρχει ένα υποσύνολο του

εστω $\displaystyle \left\{a_{n}:n \in \mathbb{N} \right\}:x=\left|\left|x \right| \right|\sum_{n=1}^{\infty}{\left(\frac{1}{2} \right)^{n-1}a_{n}}$ . Eπομένως η απεικόνιση $\displaystyle \mathbb{\phi}:l_{1}\left(\mathbb{N} \right)\times \mathcal{M_{W}} \rightarrow X$ με τύπο $\displaystyle \phi\left(\left(a_{n} \right)_{n},\left(z_{n} \right)_{n} \right)=\sum_{n=1}^{\infty}{a_{n}z_{n}}$ , (με $\mathcal{M_{W}}$ το σύνολο των ακολουθιών με στοιχεία από το

), είναι καλά ορισμένη (αφού ο χώρος είναι πλήρης άρα μια απολύτως συγκλίνουσα σειρά συγλίνει ), και επί από την παραπάνω παρατήρηση.Επομένως από γνωστό πόρισμα της θεωρίας συνόλων έχουμε $\displaystyle \left|X \right|\leq \left|l_{1}\left(\mathbb{N} \right)\times \mathcal{M_{W}} \right|$ , και $\displaystyle \left|l_{1}\left(\mathbb{N} \right) \right|=\left|\mathbb{R^{\mathbb{N}}} \right|=\left|\mathbb{R} \right|^{\mathbb{N}}=2^{\left|\mathbb{N}\times \mathbb{N} \right||}=\left|\mathbb{R} \right|$ (από ιδιότητες πληθαρίθμων) καθώς επίσης $\displaystyle \left|\mathcal{M_{W}} \right|=\left|\mathbb{N}^{\mathbb{N}} \right| =\left|\mathbb{R} \right|$ .Τελικά $\displaystyle \left|X \right|\leq \left|\mathbb{R} \right|$ και άρα $\displaystyle \dim X\leq \left|\mathbb{R} \right|$ .Τελικά χρησιμοποιώντας το πρώτο ερώτημα και το θεώρημα Cantor-Bernstein έχουμε $\displaystyle \dim X=\left|\mathbb{R} \right|$ .

Edit: Δείτε και εδώ: http://www-dimat.unipv.it/giulio/linked ... aHamel.pdf

Γ.-Σ. Σμυρλής · #3

Δυστυχῶς δέν ἐπιτρέπεται ἡ χρήση τῆς Ὑποθέσεως τοῦ Συνεχοῦς - Ἄν ἐπετρέπετο, τότε τό πρῶτο ἐρώτημα θά ἦταν προφανές!

kwstas12345 · #4

Συμφωνώ ότι η υπόθεση του συνεχούς κάνει τα πράγματα αρκετά εύκολα, ωστόσο όχι τετριμμένα μιας και χρειάζεται να ξέρει κανείς το θεώρημα Baire για να δείξει ότι ένας πλήρης χώρος έχει υπεραριθμίσιμη βάση Hamel.Παραθέτω ένα σύνδεσμο για την απόδειξη του α: http://user.math.uzh.ch/halbeisen/publi ... /hamel.pdf

Διάσταση χώρου Banach

Διάσταση χώρου Banach

Re: Διάσταση χώρου Banach

Re: Διάσταση χώρου Banach

Re: Διάσταση χώρου Banach

Μέλη σε σύνδεση