 . Ορίζουμε την ομάδα:
. Ορίζουμε την ομάδα:
Να δειχθεί ότι
 όπου
όπου  η διεδρική ομάδα.
η διεδρική ομάδα.Συντονιστής: Demetres
 ή ισοδύναμα την
ή ισοδύναμα την  , μπορούμε να γράψουμε κάθε στοιχείο του
, μπορούμε να γράψουμε κάθε στοιχείο του  στη μορφή
στη μορφή  για
για  . Χρησιμοποιώντας το
. Χρησιμοποιώντας το  μπορούμε να υποθέσουμε ότι
μπορούμε να υποθέσουμε ότι  . Χρησιμοποιώντας το
. Χρησιμοποιώντας το  μπορούμε να υποθέσουμε ότι
μπορούμε να υποθέσουμε ότι 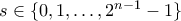 .
. .
.  . Ισχυριζόμαστε ότι
. Ισχυριζόμαστε ότι  . Σίγουρα
. Σίγουρα  . Επίσης,
. Επίσης,  αφού:
αφού:
 (με
(με 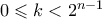 ), τότε
), τότε 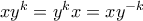 οπότε
οπότε  και άρα
και άρα 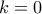 ή
ή  .
. , τότε
, τότε  οπότε
οπότε  , άτοπο αφού
, άτοπο αφού  .
. η οποία είναι η διεδρική ομάδα με
η οποία είναι η διεδρική ομάδα με  στοιχεία.
στοιχεία.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης